# 問題
あるヒストグラムを考えよう.そのヒストグラムを容器に見立てて上から水を流し込む.このとき,ヒストグラム内に貯まる水の量はいくつか.
入力としてヒストグラムはリストの形で与えられる.
| |
# 時間計算量$O(n^2)$・空間計算量$O(1)$な答え
ある位置iで溜まる水の高さは,その位置から左右両側を見て,その位置より高い地点があるならそれらの低い方の高さになる.これを各位置について計算する.
| |
# 時間計算量$O(n)$・空間計算量$O(n)$な答え
ある位置iから見て左右の高さの最大値は,位置i - 1でのそれと位置iの高さのうちの高い方なので,左右から「その位置での直近の最大値」を計算し,各位置で小さい方を取れば水面の高さが取れる.max_by_left/max_by_rightを真面目に求めるのではなくて直近との比較で時間効率良く求めるというのがこのやり方.
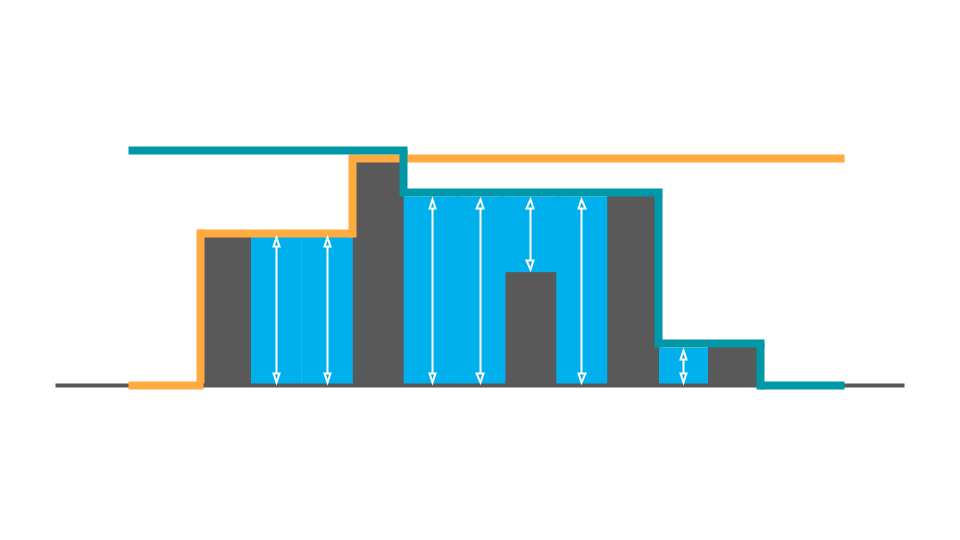
アルゴリズム概観
| |
| |
# 時間計算量$O(n)$・空間計算量$O(1)$な答え
左右から同時に高さを求めていくことで空間計算量を削減する.左右からポインタを交差するまで走らせ,走らせながら高さを確定させていく.
| |
# 類題
3 次元のヒストグラムが与えられたときの溜まる水の量を計算せよ.
| |
# 類題答え
外堀から埋めていく.
| |
