Range Query

「与えられた配列に対して，ある範囲についての大量のクエリを処理しろ」というときには以下のテクニックが有効．基本的には「大量のクエリ」を処理するために，$O(N)$ぐらいの前処理をしてクエリ自体には$O(1)$で答えられるようにするというのが基本戦略．

  • 累積和
  • Binary Index Tree
  • Segment Tree

# 累積和

「累積和の差」が「範囲の和」になるということを利用．累積和の作り方は添字が煩雑になりやすいので，次のように作ると決めてしまうと楽．

長さNの整数配列arrの累積和accumは

  • accum[0] = 0
  • accum[i+1] = accum[i] + arr[i]

このとき，範囲[left, right)について

  • arr[left:right] = accum[right] - accum[left]

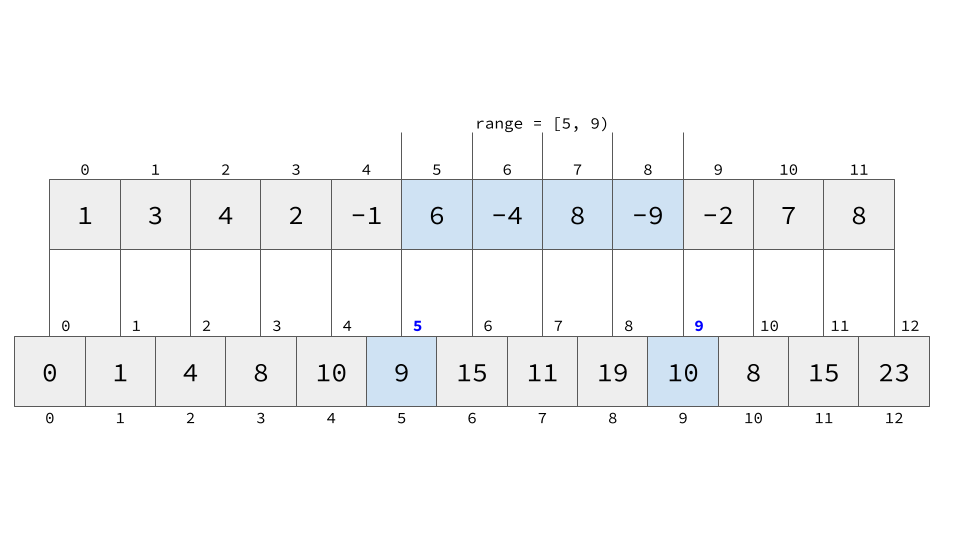
累積和

ここで意識すべきは，

  • accum[0] = 0
  • 範囲は右開区間
    • 問題上で範囲が与えられるときは左右閉区間で与えられることが多いので，その時はaccumにアクセスするタイミングで1足すなりして対応する

# 例題1

長さ$N$の整数列$A$があります．$A$の空でない連続する部分列であって，その総和が$0$になるものの個数を求めてください．ただし，ここで数えるのは部分列の取り出し方であることに注意してください．つまり，ある$2$つの部分列が列として同じでも，取り出した位置が異なるならば，それらは別々に数えるものとします．

from https://atcoder.jp/contests/agc023/tasks/agc023_a

累積和をとって，集計する．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

from collections import Counter
N = int(input())
A = list(map(int, input().split(" ")))
accum = [0 for _ in range(len(A) + 1)]
for i in range(len(A)):
    accum[i+1] = accum[i] + A[i]

freq = Counter(accum)
ans = 0
for v in freq.values():
    ans += v * (v - 1) / 2

print(ans)

# 例題2

Given an integer array nums, handle multiple queries of the following type:

Calculate the sum of the elements of nums between indices left and right inclusive where left <= right. Implement the NumArray class:

  • NumArray(int[] nums) Initializes the object with the integer array nums.
  • int sumRange(int left, int right) Returns the sum of the elements of nums between indices left and right inclusive (i.e. nums[left] + nums[left + 1] + ... + nums[right]).

from https://leetcode.com/problems/range-sum-query-immutable/

まさしく累積和を使ってほしいという意図が見える問題．問題文中では範囲が閉区間で行われているので，それに合わせてsumRange内でrightの扱いに注意する．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class NumArray:

    def __init__(self, nums: List[int]):
        self.nums = nums
        accums = [0 for _ in range(len(nums) + 1)]
        for i in range(0, len(nums)):
            accums[i + 1] = accums[i] + nums[i]
        self.accums = accums

    def sumRange(self, left: int, right: int) -> int:
        return self.accums[right + 1] - self.accums[left]


# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# param_1 = obj.sumRange(left,right)

# 二次元累積和

ついでなので二次元配列の累積和についても記載しておく．

二次元配列Aが与えられたときに，[x1, x2) x [y1, y2)である長方形の範囲内の要素の総和を求めるクエリを考える．

累積和accumは

  • accum[0][0] = 0
  • accum[i][j] = [0, i) x [0, j)の長方形範囲の総和
    • accum[i+1][j+1] = accum[i+1][j] + accum[i][j+1] - accum[i][j] + A[i][j]

こうすることで，[x1, x2) x [y1, y2)である長方形の範囲内の要素の総和は，accum[x2][y2] - accum[x1][y2] - accum[x2][y1] + accum[x1][y1]で求められる．

# 例題

Given a 2D matrix matrix, handle multiple queries of the following type:

Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2). Implement the NumMatrix class:

NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix. int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

from https://leetcode.com/problems/range-sum-query-2d-immutable/

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        self.matrix = matrix
        H = len(matrix)
        W = len(matrix[0])
        accum = [[0 for _ in range(W + 1)] for _ in range(H + 1)]
        for h in range(0, H):
            for w in range(0, W):
                accum[h + 1][w + 1] = accum[h][w + 1] + accum[h + 1][w] - accum[h][w] + matrix[h][w]
        self.accum = accum

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        row2 += 1
        col2 += 1
        return self.accum[row2][col2] - self.accum[row2][col1] - self.accum[row1][col2] + self.accum[row1][col1]


# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)

# Segment Tree

配列を「区間」を単位に完全二分木で管理する．

1-indexな配列上に完全二分木を実装する．頂点iの子供は頂点2*i，頂点2*i + 1．

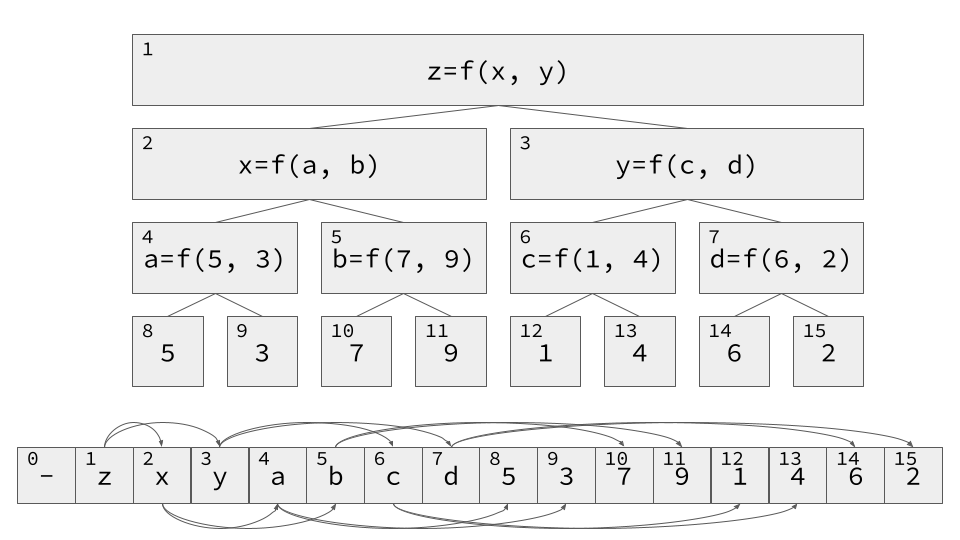
セグメント木は配列で実装する

updateクエリでは上にさかのぼっていきながら木を更新する．

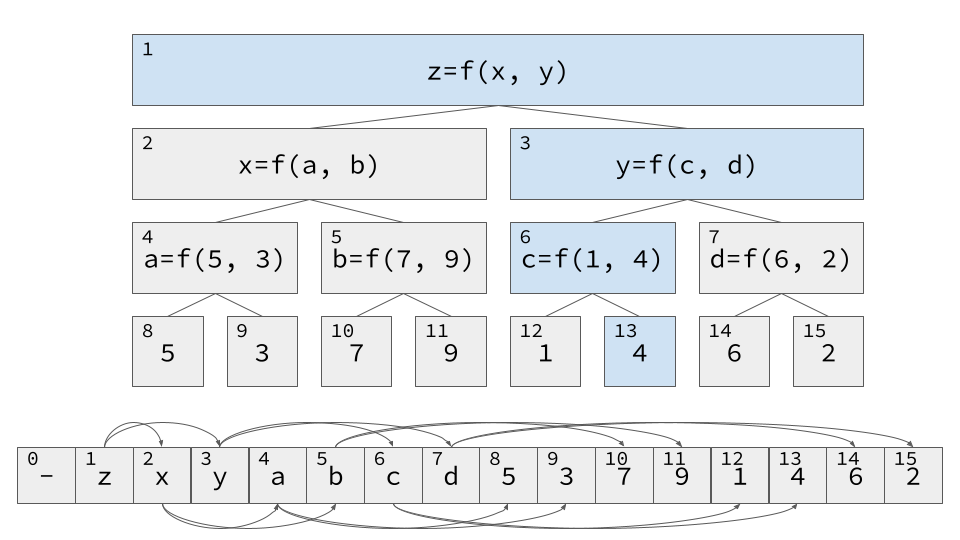
`update`クエリ系

rangeクエリでは下から該当する範囲を拾っていくイメージ．

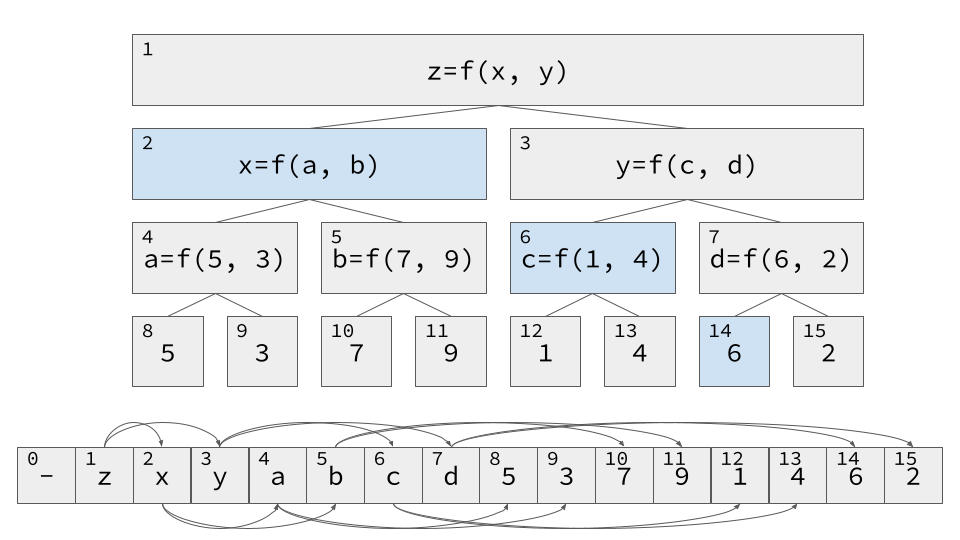
`range`クエリ系

なお，クエリ時のインデックスは0-indexであることに注意．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

class SegmentTree:
    def __init__(self, init_list, func, ele):
        """
        init_list: 管理対象の整数配列
        func:      区間に対して実行する処理（min/max/sum/productなど）
        ele:       単位元
        """
        n = len(init_list)
        self.func = func
        self.ele = ele
        self.num = 1 << (n - 1).bit_length()
        self.tree = [ele for _ in range(2 * self.num)]

        for i in range(n):
            self.tree[i + self.num] = init_list[i] # set leaf

        for i in range(self.num - 1, 0, -1):
            self.tree[i] = self.func(self.tree[2 * i], self.tree[2 * i + 1])

    def update(self, pos, val):
        """
        init_listのpos番目の要素をvalに更新
        note: posは0-origin
        """
        pos += self.num
        self.tree[pos] = val
        while 1 < pos:
            self.tree[pos >> 1] = self.func(self.tree[pos], self.tree[pos ^ 1])
            pos >>= 1

    def query(self, left, right):
        """
        init_listの[left, right)に対してfuncした結果を返す
        note: left, rightは0-origin
        """
        ret = self.ele

        left += self.num
        right += self.num

        while left < right:
            if left & 1:
                ret = self.func(ret, self.tree[left])
                left += 1
            if right & 1:
                ret = self.func(ret, self.tree[right - 1])
            left >>= 1
            right >>= 1

        return ret

lst = [5, 3, 7, 9, 1, 4, 6, 2]
seg = SegmentTree(init_list=lst, func=min, ele=float("+inf"))
print(seg.query(2, 5)) # => 1
seg.update(2, 0) # lst[2] = 0
print(seg.query(2, 5)) # => 0

# 例題

Given an integer array nums, handle multiple queries of the following types:

  1. Update the value of an element in nums.
  2. Calculate the sum of the elements of nums between indices left and right inclusive where left <= right. Implement the NumArray class:
  • NumArray(int[] nums) Initializes the object with the integer array nums.
  • void update(int index, int val) Updates the value of nums[index] to be val. int sumRange(int left, int right) Returns the sum of the elements of nums between indices left and right inclusive (i.e. nums[left] + nums[left + 1] + ... + nums[right]).

from https://leetcode.com/problems/range-sum-query-mutable/

要するにfunc=sumなセグメント木を実装しろという問題．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

class NumArray:

    def __init__(self, nums: List[int]):
        n = len(nums)
        self.num = 1 << (n - 1).bit_length()
        self.tree = [0 for _ in range(2 * self.num)]
        for i in range(n):
            self.tree[i + self.num] = nums[i]
        for i in range(self.num - 1, 0, -1):
            self.tree[i] = self.tree[2 * i] + self.tree[2 * i + 1]

    def update(self, index: int, val: int) -> None:
        index += self.num
        self.tree[index] = val
        while 1 < index:
            self.tree[index >> 1] = self.tree[index] + self.tree[index ^ 1]
            index >>= 1

    def sumRange(self, left: int, right: int) -> int:
        right += 1

        ret = 0
        left += self.num
        right += self.num
        while left < right:
            if left & 1:
                ret += self.tree[left]
                left += 1
            if right & 1:
                ret += self.tree[right - 1]
            left >>= 1
            right >>= 1
        return ret


# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# obj.update(index,val)
# param_2 = obj.sumRange(left,right)

# Binary Index Tree（BIT）

セグメント木から機能を削ぎ落とした感じ．

Binary Index Tree

  • BITは1-indexな配列上に作る
  • updateクエリ
    • 次に更新すべきBIT上の位置は，現在見ている位置にその位置が相当する区間の長さを足すと出てくる
    • BIT上の位置posについて，posの担当する範囲の長さはpos & -pos
      • posのビット列の1が立ってる一番小さい桁を取ってる
  • rangeクエリ
    • BITに対するrangeクエリは「[0, idx)の範囲の和」というクエリ
      • これを2つ組み合わせれば任意の範囲の和が取れる
      • [idx0, idx1) = [0, idx1) - [0, idx0)
    • 次に足すべきBIT上の位置は，現在見ている位置にその位置が相当する区間の長さを引くと出てくる
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class BIT:
    def __init__(self, n):
        self.size = n
        self.tree = [0 for _ in range(n + 1)] # 0で初期化

    def add(self, pos, val):
        """
        位置posの要素にvalを加える
        note: posは0-origin
        """
        while pos <= self.size:
            self.tree[pos] += val
            pos += (pos & -pos)

    def range(self, pos):
        """
        範囲[0, pos)の和を返す
        note: posは0-origin
        """
        ret = 0
        while 0 < pos:
            ret += self.tree[pos]
            pos -= (pos & -pos)

# Refs

© 2024 Ozaki Yoichi
Hugo で構築されています。
テーマ Stack は Jimmy によって設計されています。