二分木上の探索
次のように定義される二分木を考える.
1
2
3
4
5
| class: TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
|
ある二分木rootが与えられたときに,その木を構成する頂点の全探索は「深さ優先探索 Depth-First Search(DFS)」と「幅優先探索 Breadth-First Search(BFS)」に大別される.
深さ優先探索 Depth-First Search(DFS)
二分木における深さ優先探索は「今いる頂点を調査して,その子供の頂点にも同じ調査を繰り返すように走査」する.
今いる頂点と左右の子供の頂点をどういう順番で走査するのかで名前が付いている.
- 行きがけ順(pre-order traversal)
- まず根ノードを見て,続けて左部分木を行きがけ順で走査,最後に右部分機を行きがけ順で走査
- 通りがけ順(in-order traversal)
- まず左部分機を通りがけ順で走査,続けて根ノードを見て,最後に右部分機を行きがけ順で走査
- 帰りがけ順(post-order traversal)
- まず左部分機を通りがけ順で走査,続けて右部分機を行きがけ順で走査,最後に根ノードを見て
再帰関数で簡単に実装することができる.stackを用いても実装可能.
行きがけ順を再帰関数で実装すると
1
2
3
4
| def preorder(root):
process(root)
preorder(root.left)
preorder(root.right)
|
行きがけ順をstackを用いて実装すると
1
2
3
4
5
6
7
| def preorder(root):
stack = [root]
while len(stack) != 0:
node = stack.pop()
process(node)
stack.append(root.left)
stack.append(root.right)
|
通りがけ順を再帰関数で実装すると
1
2
3
4
| def inorder(root):
preorder(root.left)
process(root)
preorder(root.right)
|
帰りがけ順を再帰関数で実装すると
1
2
3
4
| def inorder(root):
preorder(root.left)
preorder(root.right)
process(root)
|
幅優先探索 Breadth-First Search(BFS)
二分木における幅優先探索は「深さが同じ頂点群を,浅い順に走査」する.queueを用いると簡単に実装できる.
1
2
3
4
5
6
7
| def bfs(root):
queue = [root]
while len(queue) != 0:
node = queue.pop(0)
process(node)
queue.append(root.left)
queue.append(root.right)
|
Morris Traversal
再帰関数による(行きがけ順|通りがけ順|帰りがけ順)DFS,stackによる(行きがけ順)DFS,queueによるBFSは,木を構成する頂点の総数が$n$であるとして,
- 時間計算量$O(n)$
- 空間計算量$O(\log n)$
- 木の高さ(=$\log n$)分call stack/stack/queueが伸びるから
Morris traversalアルゴリズムは時間計算量$O(n)$,空間計算量を$O(1)$で木を構成する頂点を通りがけ順で全探索するアルゴリズム.
「左部分木の左端の葉ノードに到達するまでに間に,左部分木の右端葉ノードから通りがけ順で直後の頂点へのポインタを(右の子供として)張りながら木を降りていって,降りきれなくなったタイミングでひたすら右の子供をたどっていくと,通りがけ順になってる」というもの.
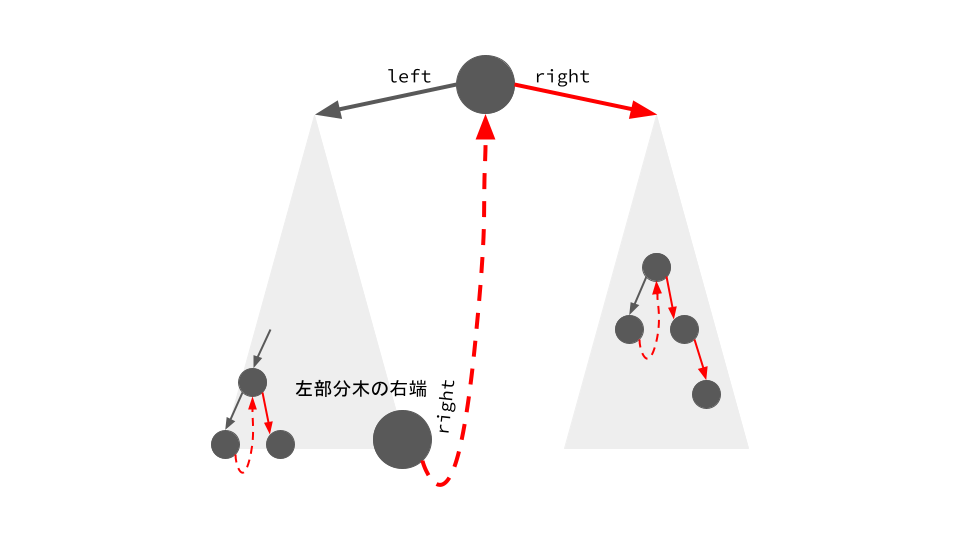
Morris Traversalの概要
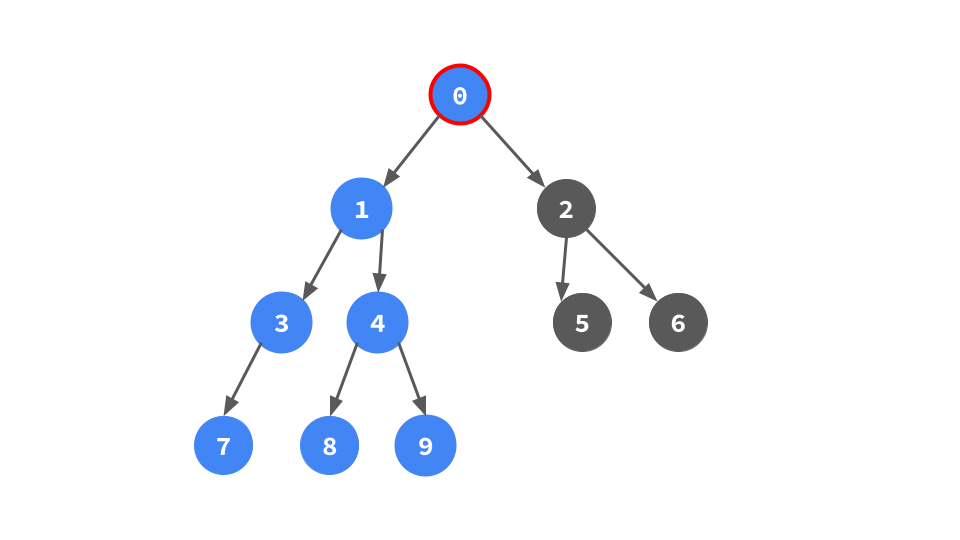
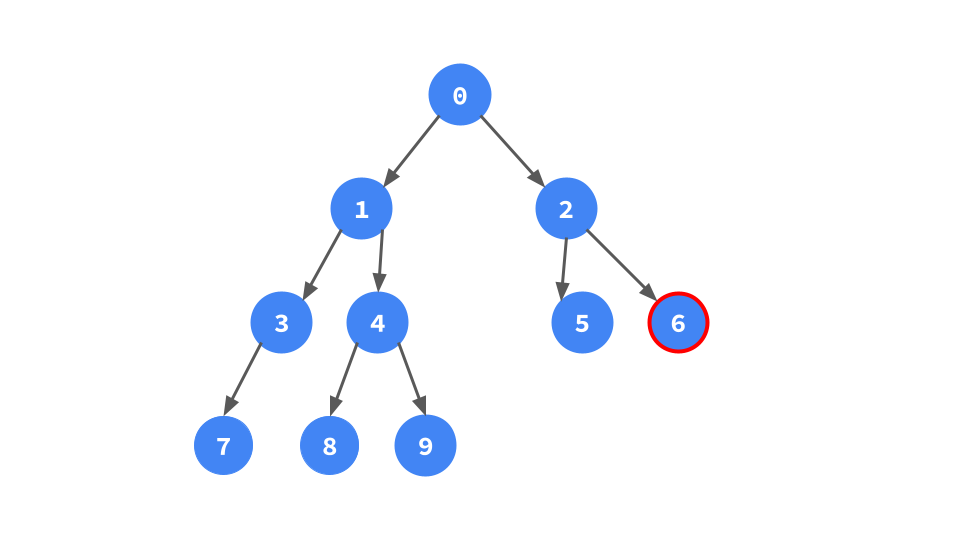
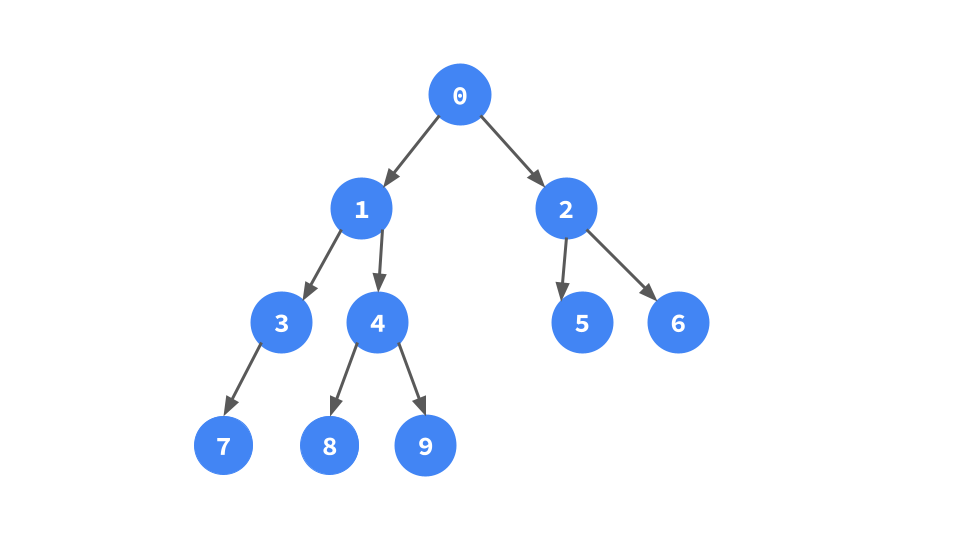
次に示す具体例で動作を追っていく.
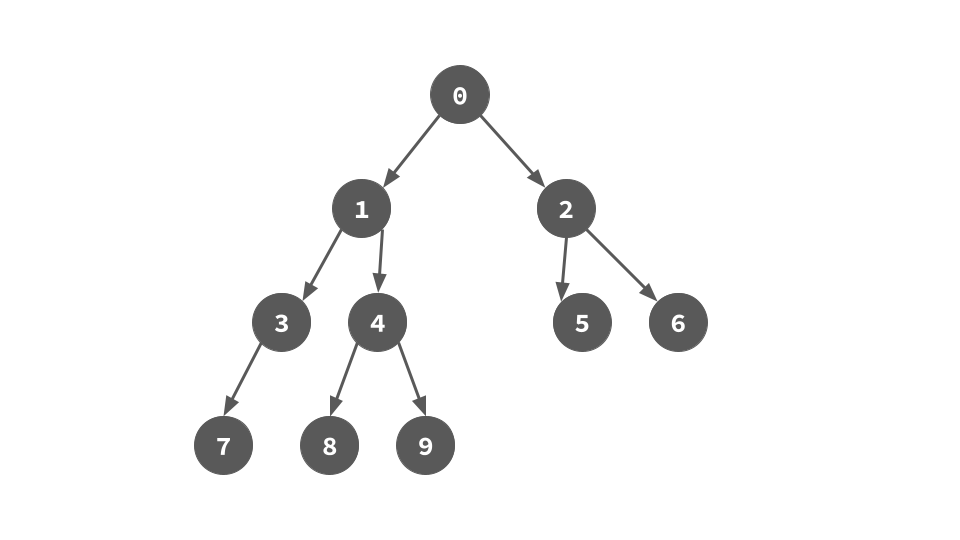
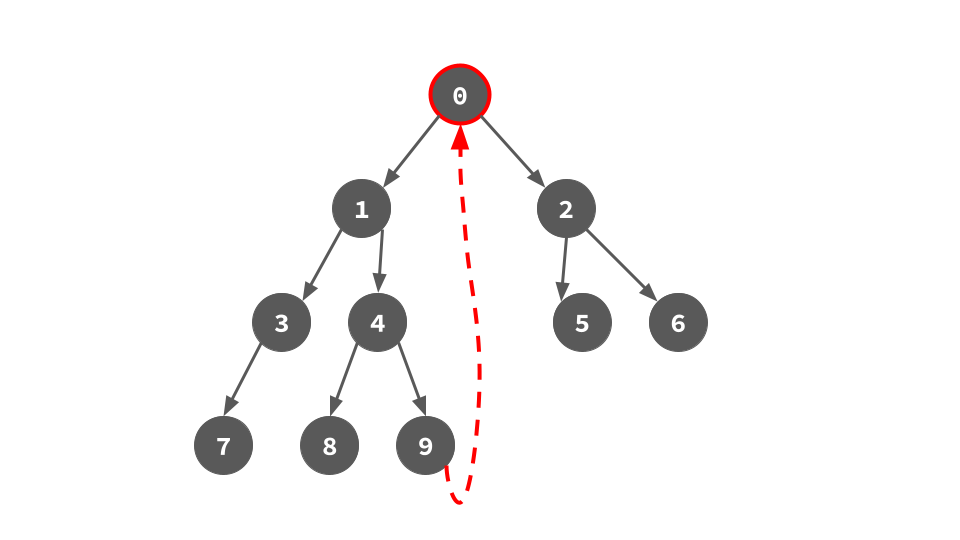
まず頂点0から走査を始める.0には左部分木があるので,0の左部分木の右端葉を計算すると今回は頂点9.9の右の子供として0へのポインタを張っておく.このポインタを後でたどることで行きがけ順を達成する.
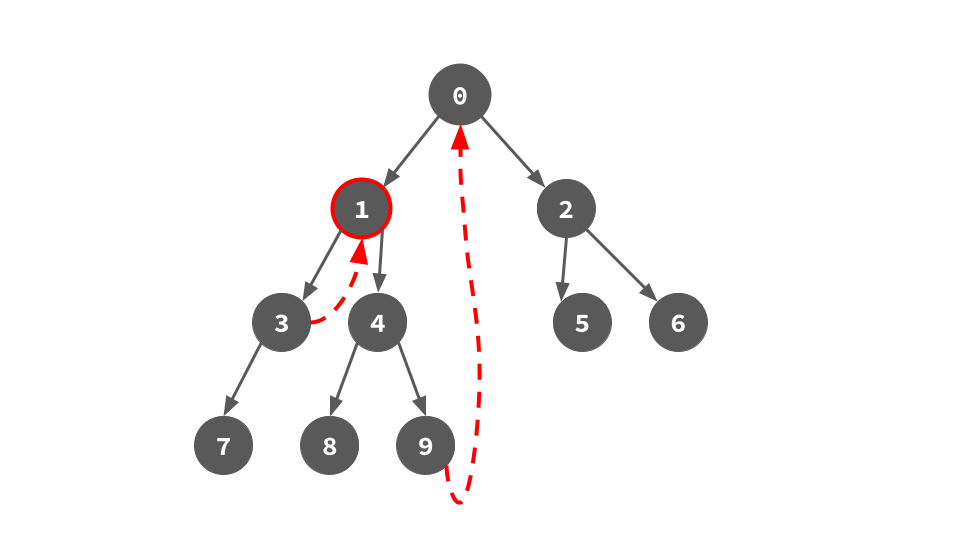
0の左部分木へ降りていき,降り立った頂点を根とした木の左部分木が存在するる限り同じように「左部分木の右端葉を計算して,それの右の子供として根へのポインタを張る」ことを繰り返す.
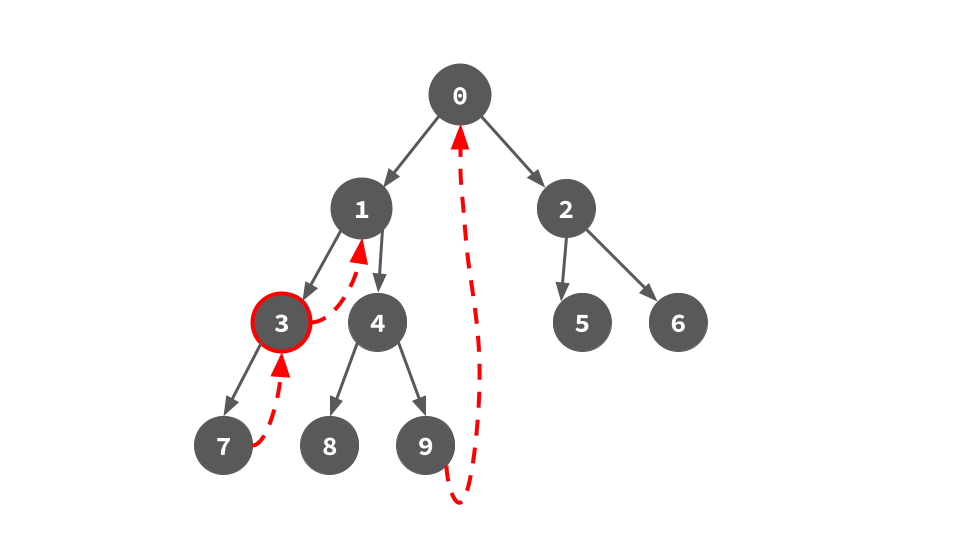
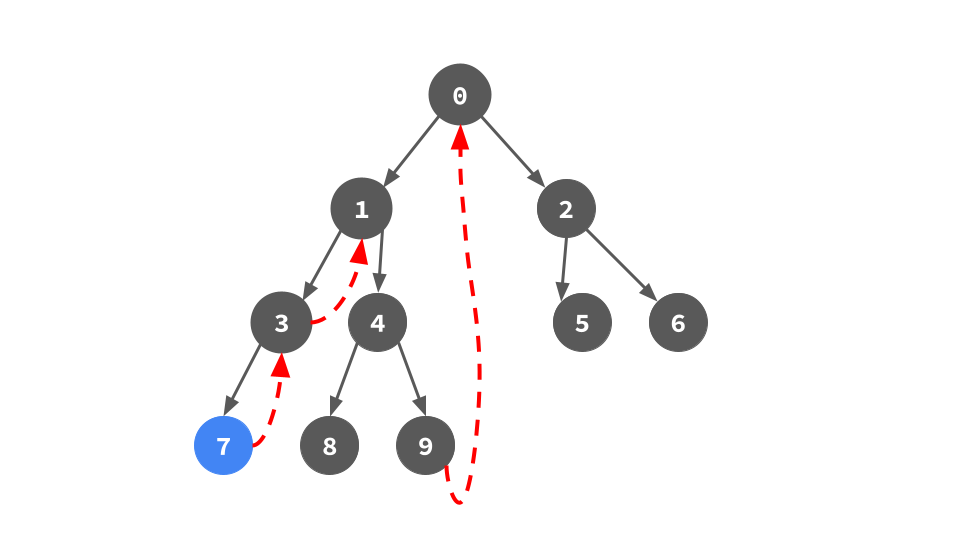
左部分機が存在しない,つまり左端の葉まで降りたら,そこが行きがけ順の一番最初の頂点なので処理をする.今回は頂点7がそれ.頂点7を処理したら,さっき張った7の右子ポインタを使って遷移する.このポインタは行きがけ順における左部分期の右端葉とその直後の頂点を結んでいるので正しく行きがけ順に遷移することになる.今回の例だと3へ赤いポインタを使って遷移することになる.このとき,遷移しながら赤いポインタを剥がす,具体的には7の右子ポインタにNoneをセットする.このアルゴリズムでは「ポインタを張りながら遷移して不要になったらすぐ剥がす」という挙動になっている.全部張ってから剥がすのではないという点に注意.
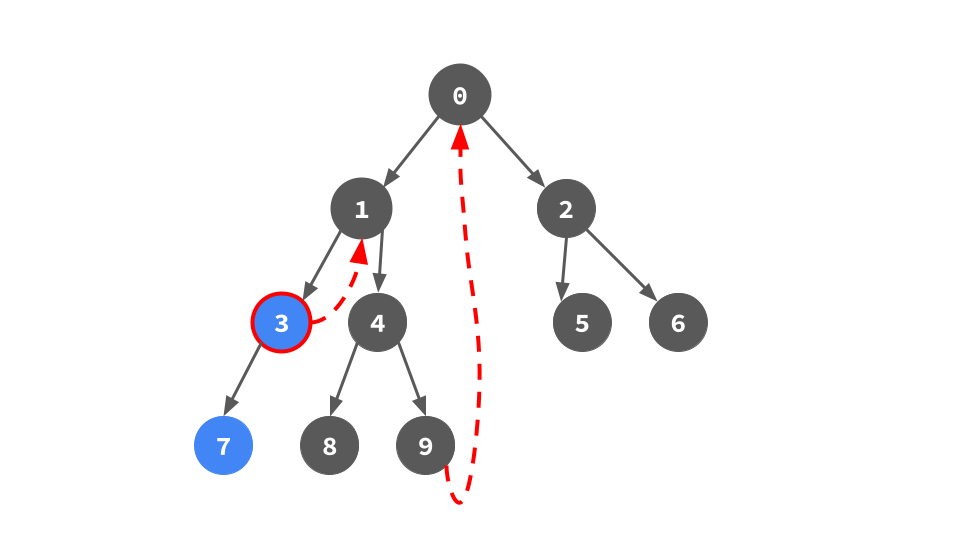
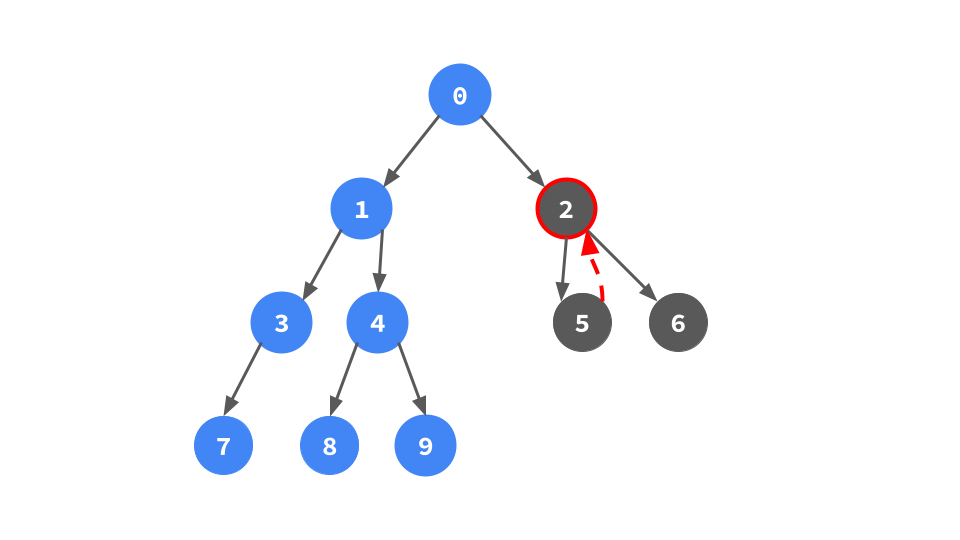
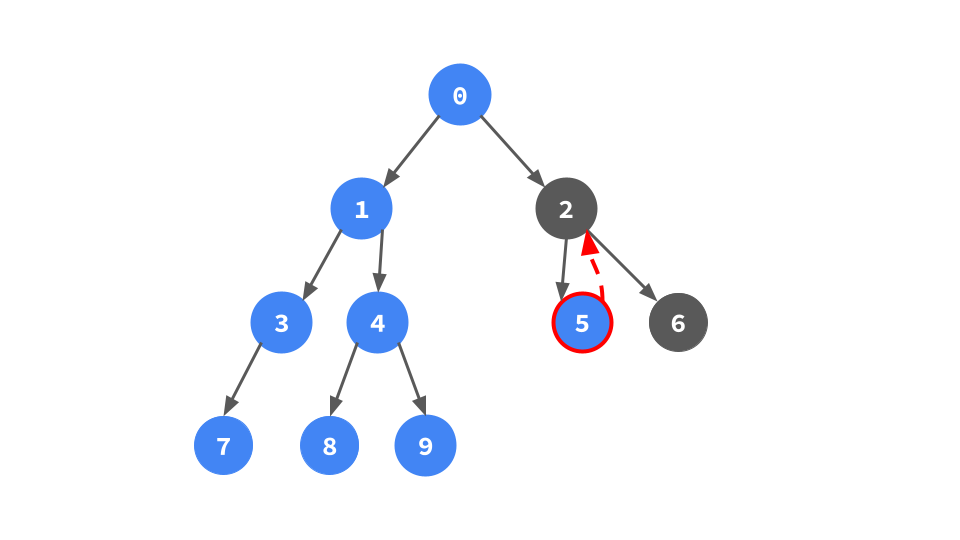
右子ポインタで次へ行く次へ行く.
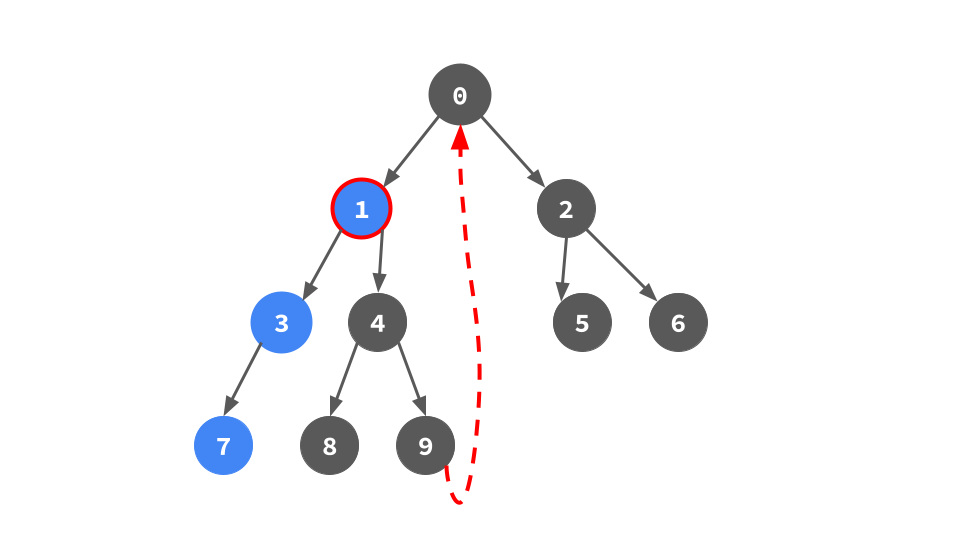
左子ポインタがあるなら,左部分木が存在するので,左部分期の右端葉頂点を見つけて行きがけ順になるためのポインタを張る作業(頂点0/1/3でやってきたのと同じこと)をやる.
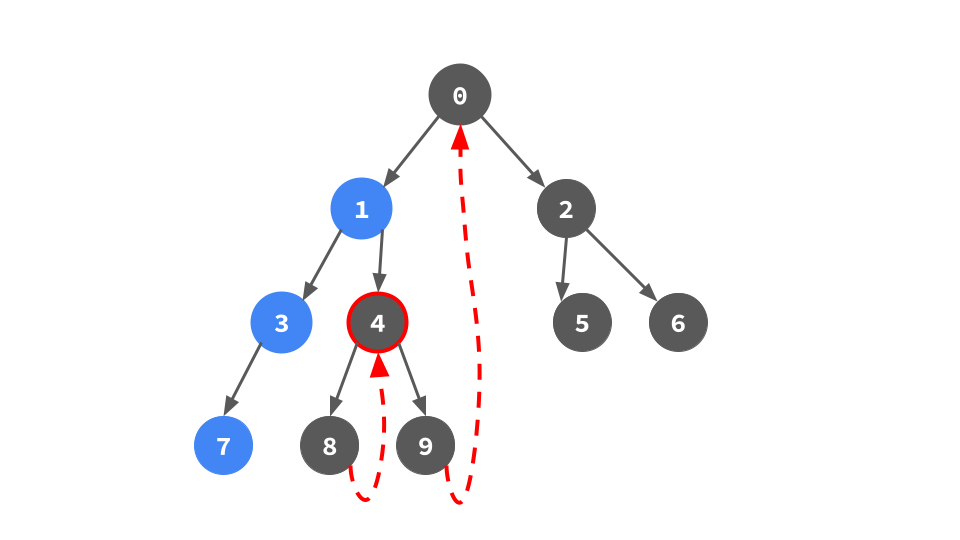
左子ポインタがないということは左部分木が存在しないので,右子ポインタをたどる.
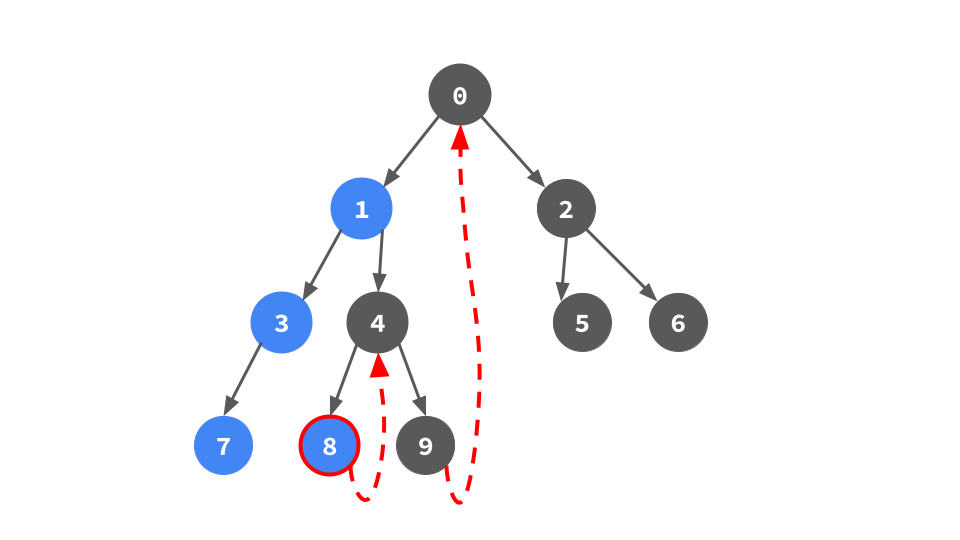
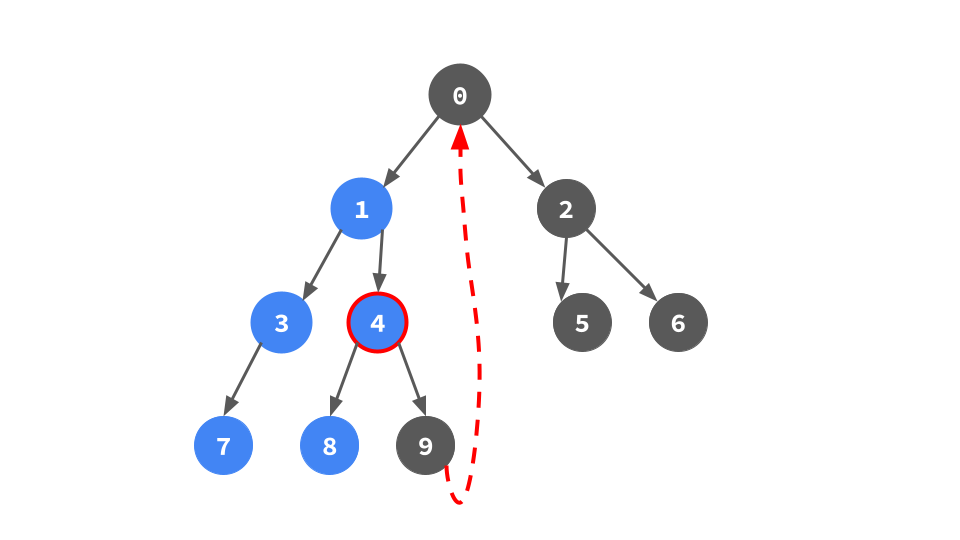
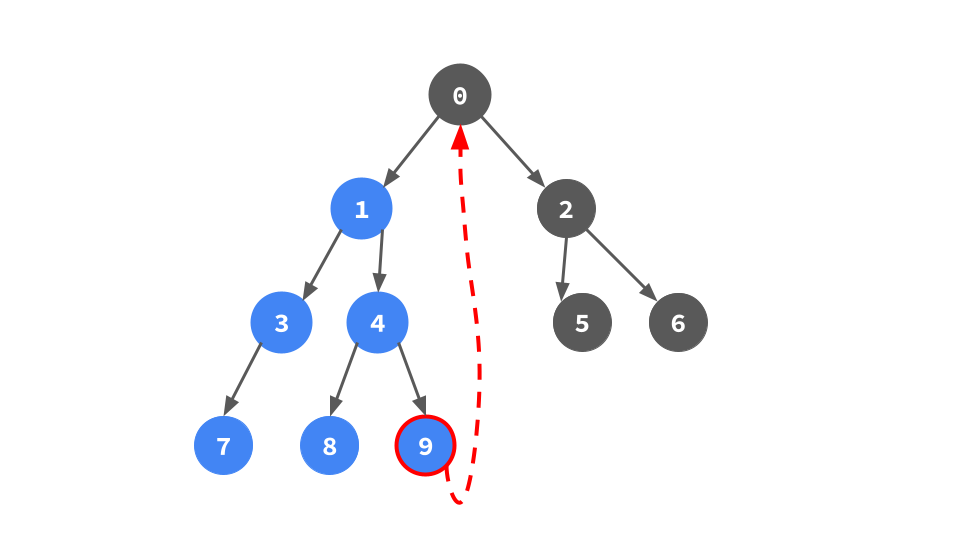
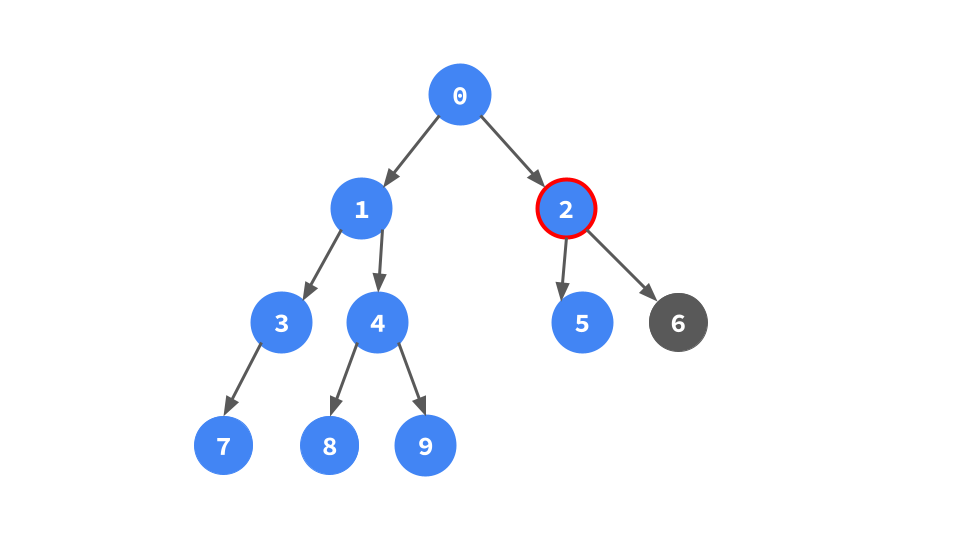
これを実装すると次のようになる.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| def morris(root):
curr = root
while curr is not None:
if curr.left is not None:
# 左部分木が存在するので,左部分期の右端葉ノードを探しに行く
prev = curr.left
while prev.right is not None and prev.right is not curr:
prev = prev.right
if prev.right is None:
prev.right = curr # 右子ポインタで行きがけ順直後の頂点を登録(赤矢印)
curr = curr.left # 左部分木へ降りていく
else: # すでに赤矢印が張ってあるということは左部分木は見終わったということになる
prev.right = None # 赤矢印を剥がす
process(curr)
curr = curr.right # 左部分木を見終わったので右部分木へ降りていく
else: # curr.left is None
process(curr)
curr = curr.right # 左部分木が存在しないので右部分木へ降りていく
|
やや複雑.これを何も見ずに書けと要求されるとしんどい.
練習問題
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| # Morris traversal:空間計算量O(1)で全頂点をin-orderで探索する.イメージとしては左部分木の右端から根への一時的なポインタを作りながら木を下に降りていき,葉ノードに到達したらそこから右へ右へ進んでいくとin-orderになっている.右へ右へ進む途中で一時的に張ったポインタを消しながら進む.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root: TreeNode) -> int:
ans = 0
while root is not None:
if root.left is not None:
prev = root.left
while prev.right is not None and prev.right is not root:
prev = prev.right
if prev.right is None: # in-order順でrootの直前のノードがprevになっている
prev.right = root # 一時的なリンクを張る
root = root.left
else:
prev.right = None # ここで一時的に張ったリンクを消してる
if prev is root.left and prev.left is None:
ans += prev.val
root = root.right
else: # ここに入り込む時点でrootは左端の葉ノード
root = root.right
return ans
|

















