この 60 問 を Python で解く.
01: Two Sum $O(n^2)$ではない答えにしたいので,どうするか.
答え 1
2
3
4
5
6
7
8
9
class Solution :
def twoSum ( self , nums : List [ int ], target : int ) -> List [ int ]:
table = dict ()
for idx , num in enumerate ( nums ):
complement = target - num
if complement in table . keys ():
return [ idx , table [ complement ]]
else :
table [ num ] = idx
02: Add Two Numbers 再帰的に書く.再帰的に.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution :
def addTwoNumbers ( self , l1 : ListNode , l2 : ListNode ) -> ListNode :
def _recurse ( l1 : ListNode , l2 : ListNode , carry : int ) -> ListNode :
# base case
if l1 is None and l2 is None and carry == 0 :
return None
val = carry
if l1 is not None :
val += l1 . val
if l2 is not None :
val += l2 . val
result = ListNode ( val = val % 10 , next = None )
if l1 is not None or l2 is not None :
next_l1 = None
next_l2 = None
if l1 is not None :
next_l1 = l1 . next
if l2 is not None :
next_l2 = l2 . next
next_carry = val // 10
result . next = _recurse ( next_l1 , next_l2 , next_carry )
return result
return _recurse ( l1 , l2 , 0 )
リストが「桁の大きい順」になっている場合はリストを逆転させてこの問題に帰着させるか,スタックを 2 つ使う方法がある.
リストを逆転させる解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution :
def addTwoNumbers ( self , l1 : ListNode , l2 : ListNode ) -> ListNode :
def reverse ( root ):
if root is None or root . next is None :
return root
reversed_head = reverse ( root . next )
root . next . next = root
root . next = None
return reversed_head
def rec ( l1 , l2 , carry ):
if l1 is None and l2 is None and carry == 0 :
return None
val = carry
val += l1 . val if l1 is not None else 0
val += l2 . val if l2 is not None else 0
ret = ListNode ( val = val % 10 , next = None )
l1_next = l1 . next if l1 is not None else None
l2_next = l2 . next if l2 is not None else None
ret . next = rec ( l1_next , l2_next , val // 10 )
return ret
return reverse ( rec ( reverse ( l1 ), reverse ( l2 ), 0 ))
2 つのスタックを使う解法:スタックを使うことで数字を小さい桁から扱えるようになる.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution :
def addTwoNumbers ( self , l1 : ListNode , l2 : ListNode ) -> ListNode :
stack1 = []
stack2 = []
while l1 is not None :
stack1 . append ( l1 . val )
l1 = l1 . next
while l2 is not None :
stack2 . append ( l2 . val )
l2 = l2 . next
carry = 0
head = None
while len ( stack1 ) != 0 or len ( stack2 ) != 0 or carry != 0 :
val = carry
val += stack1 . pop () if stack1 else 0
val += stack2 . pop () if stack2 else 0
carry = val // 10
head_new = ListNode ( val = val % 10 , next = head )
head = head_new
return head
03: Longest Substring Without Repeating Characters 題意は「与えられた文字列に含まれる,ユニークな文字による連続する部分文字列の中で,最長のものの長さを求めよ」
答え これはしゃくとり法.すでに見たことのある文字が出てきた次点で,それを含む範囲を伸ばしても答えにならないので,走査範囲の左端を右端の隣に更新する.$O(n)$.
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution :
def lengthOfLongestSubstring ( self , s : str ) -> int :
# しゃくとり法
start = 0
max_len = 0
seen = dict () # {char: occurrence idx}
for curr , char in enumerate ( s ):
if char in seen and start <= seen [ char ]:
start = seen [ char ] + 1
else :
max_len = max ( max_len , curr - start + 1 )
seen [ char ] = curr
return max_len
04: ZigZag Conversion 観察する.
1
2
3
4
row = 0 | 0 -( +6) -> 6
row = 1 | 1 -( +4) -> 5 -( +2) -> 7 ...
row = 2 | 2 -( +2) -> 4 -( +4) -> 8 10
row = 3 | 3 -( +6) -> 9
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution :
def convert ( self , s : str , numRows : int ) -> str :
if numRows == 1 :
return s
interval = 2 * numRows - 2
ans = ""
for row in range ( numRows ):
for index in range ( row , len ( s ), interval ):
ans += s [ index ]
if not ( row == 0 or row == numRows - 1 ):
if index + ( interval - row * 2 ) < len ( s ):
ans += s [ index + ( interval - row * 2 )]
return ans
05: String to Integer (atoi) 一文字ずつ見ていく.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution :
def myAtoi ( self , s : str ) -> int :
s = s . strip ()
int_part = ""
for char in s :
if char == "." :
break # 123.4...
if char . isdigit () or char in [ "+" , "-" ]:
if char in [ "+" , "-" ] and 0 < len ( int_part ):
break # 12345+...
int_part += char
else :
break # char is alphabet
ans = 0
digit = 0
for char in int_part [:: - 1 ]:
if char == "-" :
ans *= - 1 #-123
elif char == "+" :
continue # +123
else :
ans += int ( char ) * ( 10 ** digit )
digit += 1
if - 2 ** 31 <= ans and ans < 2 ** 31 :
return ans
elif ans < - 2 ** 31 :
return - 2 ** 31
else :
return 2 ** 31 - 1
06: Valid Parentheses 閉じカッコに対応するのは,最直近の開きカッコなので,FIFO.だから stack でうまく書ける.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution :
def isValid ( self , s : str ) -> bool :
stack = []
for p in s :
if p in [ "(" , "{" , "[" ]:
stack . append ( p )
continue
else :
if len ( stack ) == 0 :
return False
q = stack . pop ()
if q in [ ")" , "}" , "]" ]:
return False
else :
if q + p in [ "()" , " {} " , "[]" ]:
continue
else :
stack . append ( q )
stack . append ( p )
if len ( stack ) == 0 :
return True
else :
return False
07: Generate Parentheses $n$個の()を正しく並べるときの全通りを出力する.
答え まず左カッコが足りないから並べて,左カッコ書きすぎたら右カッコ書いて閉じなきゃ…
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution :
def generateParenthesis ( self , n : int ) -> List [ str ]:
ret = []
def rec ( left , right , sofar ):
if left == n and right == n :
ret . append ( sofar )
return
if left < n :
rec ( left + 1 , right , sofar + "(" )
if right < left :
rec ( left , right + 1 , sofar + ")" )
rec ( 0 , 0 , "" )
return ret
08: Next Permutation 0125330の直後の順列は0130235.直後の順列は後半だけいじりたい.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution :
def nextPermutation ( self , nums : List [ int ]) -> None :
"""
Do not return anything, modify nums in-place instead.
"""
i = len ( nums ) - 1
while 0 < i and nums [ i - 1 ] >= nums [ i ]:
i -= 1
if i == 0 :
nums . reverse ()
return
i -= 1
pivot = nums [ i ]
j = len ( nums ) - 1
while pivot >= nums [ j ]:
j -= 1
nums [ i ], nums [ j ] = nums [ j ], nums [ i ]
nums [ i + 1 :] = reversed ( nums [ i + 1 :])
09: Search in Rotated Sorted Array 昇順になっているときは二分探索を使ってほしいという出題意図を汲み取りたい.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution :
def search ( self , A : List [ int ], target : int ) -> int :
n = len ( A )
left , right = 0 , n - 1
if n == 0 : return - 1
while left <= right :
mid = left + ( right - left ) // 2
if A [ mid ] == target : return mid
if A [ mid ] >= A [ left ]:
if A [ left ] <= target < A [ mid ]:
right = mid - 1
else :
left = mid + 1
else :
if A [ mid ] < target <= A [ right ]:
left = mid + 1
else :
right = mid - 1
return - 1
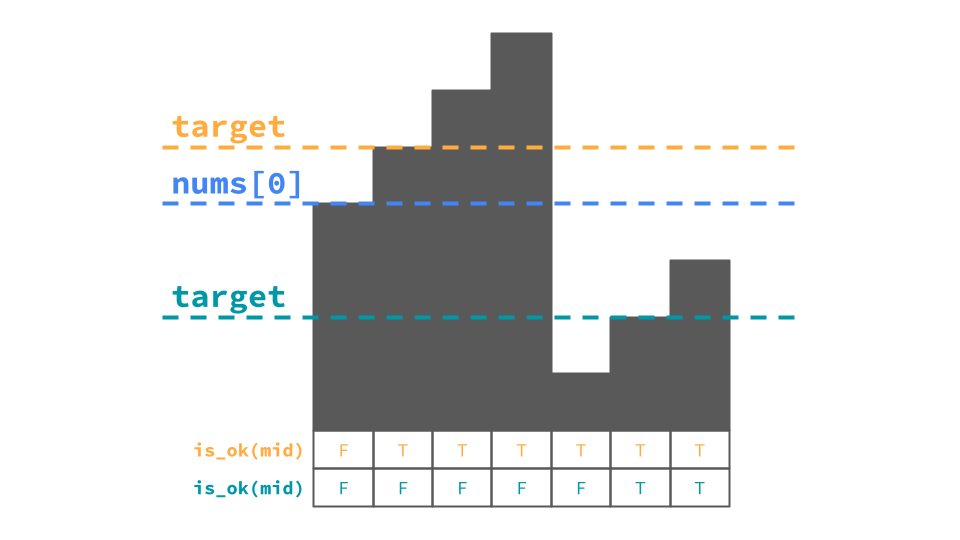
めぐる式二分探索に落とし込むことで解くほうが頭が整理されて良い.ここでは次の図のようにis_ok(mid)を設計している.
`is_ok(mid)`の挙動 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution :
def search ( self , nums : List [ int ], target : int ) -> int :
if nums [ 0 ] == target :
return 0
def is_ok ( mid ):
if nums [ 0 ] < target :
return target <= nums [ mid ] or nums [ mid ] < nums [ 0 ]
else :
return target <= nums [ mid ] and nums [ mid ] < nums [ 0 ]
ng = - 1
ok = len ( nums )
while 1 < abs ( ng - ok ):
mid = ( ng + ok ) // 2
if is_ok ( mid ):
ok = mid
else :
ng = mid
if ok < 0 or len ( nums ) <= ok or nums [ ok ] != target :
return - 1
else :
return ok
10: Search Insert Position 「要素が昇順に並んでいる」と来れば…
答え 要素が昇順に並んでいるので,二分探索.
1
2
3
class Solution :
def searchInsert ( self , nums : List [ int ], target : int ) -> int :
return bisect_left ( nums , target )
めぐる式二分探索ではこうなる.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution :
def searchInsert ( self , nums : List [ int ], target : int ) -> int :
def is_ok ( mid ):
return target <= nums [ mid ]
ng = - 1
ok = len ( nums )
while 1 < abs ( ng - ok ):
mid = ( ng + ok ) // 2
if is_ok ( mid ):
ok = mid
else :
ng = mid
return ok
別解として一つずつ見ていくのでも解ける.$O(n)$.
1
2
3
4
5
6
7
8
9
class Solution :
def searchInsert ( self , nums : List [ int ], target : int ) -> int :
pos = 0
for ele in nums :
if target <= ele :
return pos
else :
pos += 1
return pos
11: Combination Sum 全通りがいくつあるのかはわからないけど,猪突猛進に調べる.candidates[:]を使う場合,candidates[1:]を使う場合,candidates[2:]を使う場合…
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution :
def combinationSum ( self , candidates : List [ int ], target : int ) -> List [ List [ int ]]:
ret = []
def rec ( nums , remain , sofar ):
if remain < 0 :
return
if remain == 0 :
ret . append ( sofar )
return
for i in range ( len ( nums )):
rec ( nums [ i :], remain - nums [ i ], sofar + [ nums [ i ]])
rec ( candidates , target , [])
return ret
12: Permutations 集合$A$から一つ選んで,残りから一つ選んで…
答え 1
2
3
4
5
6
7
8
9
10
11
class Solution :
def permute ( self , nums : List [ int ]) -> List [ List [ int ]]:
ans = []
def _recurse ( nums , sofar ):
if len ( nums ) == 0 :
ans . append ( sofar )
return
for i in range ( len ( nums )):
_recurse ( nums [: i ] + nums [ i + 1 :], sofar + [ nums [ i ]])
_recurse ( nums , [])
return ans
13: Group Anagrams 答え 1
2
3
4
5
6
7
8
9
10
class Solution :
def groupAnagrams ( self , strs : List [ str ]) -> List [ List [ str ]]:
table = dict ()
for s in strs :
ss = "" . join ( sorted ( s ))
if ss not in table :
table [ ss ] = [ s ]
else :
table [ ss ] . append ( s )
return list ( table . values ())
14: Pow(x, n) myPow = powは流石にチートか.出題意図は繰り返し自乗法.
答え 再帰で書いた答え
1
2
3
4
5
6
7
8
9
class Solution :
def myPow ( self , x : float , n : int ) -> float :
if n == 0 :
return 1.0
if n < 0 :
return 1 / self . myPow ( x , - n )
if n % 2 == 1 :
return x * self . myPow ( x , n - 1 )
return self . myPow ( x * x , n // 2 )
繰り返しで書いた答え
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution :
def myPow ( self , x : float , n : int ) -> float :
if n == 0 :
return 1.0
if n < 0 :
x = 1 / x
n = - n
ans = 1
while n != 0 :
if n & 1 :
ans *= x
x *= x
n >>= 1
return ans
15: Maximum Subarray 答え 最大部分配列問題:与えられた配列に対して,その部分配列のうち要素の和が最大となるときのその最大和を求める問題
入力: ${a_i}_{i=0}^{n-1}$
出力: $x = \max \sum_{k=i}^j a_k \mathrel{\bigg|} 0\leq i \leq j \lt n$
$i$,$j$について全探索すれば$O(n^3)$:$x = \max_{0\leq i < n} \max_{i \leq j < n} \sum_{k=i}^j a_k$
$\sum_{k=i}^j a_k$を累積和を使って求めれば$O(n^2)$
$i$と$j$の最大値を取る順番を逆にして$x = \max_{0\leq j < n} \max_{0 \leq i < j} \sum_{k=i}^j a_k$と変形すると$s_j = \max_{0 \leq i < j} \sum_{k=i}^j a_k$として$x = \max_{0\leq j < n} s_j$となって,$s_j$について以下が成立するので$O(n)$.
$$
\begin{align}
s_{j} &= \max_{0 \leq i \leq j} \sum_{k=i}^j a_k\\\
&= \max (\max_{0 \leq i \leq j-1} \sum_{k=i}^j a_k, \max_{j \leq i \leq j} \sum_{k=i}^j a_k) \\\
&= \max (\max_{0 \leq i \leq j-1} \sum_{k=i}^{j-1} a_k + a_j, a_j) \\\
&= \max( s_{j-1} + a_j, a_j)
\end{align}
$$
1
2
3
4
5
6
7
8
class Solution :
def maxSubArray ( self , nums : List [ int ]) -> int :
s = 0
ans = - 10 ** 5
for j in range ( len ( nums )):
s = max ( s + nums [ j ], nums [ j ])
ans = max ( ans , s )
return ans
直接的にdpで書くとこうなる.
1
2
3
4
5
6
7
8
9
class Solution :
def maxSubArray ( self , nums : List [ int ]) -> int :
# dp[i]: nums[i]が右端要素となるような連続する部分配列の和の最大値
# dp[i+1] = max(dp[i] + nums[i], nums[i])
dp = [ float ( "-inf" )] * len ( nums )
dp [ 0 ] = nums [ 0 ]
for i in range ( len ( nums ) - 1 ):
dp [ i + 1 ] = max ( dp [ i ] + nums [ i + 1 ], nums [ i + 1 ])
return max ( dp )
16: Unique Paths 中学受験の道の数え上げ問題
答え 1
2
3
4
5
6
7
8
9
class Solution :
def uniquePaths ( self , m : int , n : int ) -> int :
# dp[i][j]: number of unique paths to (i, j)
# dp[i][j] = dp[i][j-1] + dp[i-1][j]
dp = [[ 1 for _ in range ( n )] for _ in range ( m )]
for i in range ( 1 , m , 1 ):
for j in range ( 1 , n , 1 ):
dp [ i ][ j ] = dp [ i ][ j - 1 ] + dp [ i - 1 ][ j ]
return dp [ m - 1 ][ n - 1 ]
17: Unique Paths II これも中学受験で頻出のやつ.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution :
def uniquePathsWithObstacles ( self , obstacleGrid : List [ List [ int ]]) -> int :
if not obstacleGrid :
return 0
H = len ( obstacleGrid )
W = len ( obstacleGrid [ 0 ])
obstacleGrid [ 0 ][ 0 ] = 1 - obstacleGrid [ 0 ][ 0 ]
for h in range ( 1 , H ):
obstacleGrid [ h ][ 0 ] = obstacleGrid [ h - 1 ][ 0 ] * ( 1 - obstacleGrid [ h ][ 0 ])
for w in range ( 1 , W ):
obstacleGrid [ 0 ][ w ] = obstacleGrid [ 0 ][ w - 1 ] * ( 1 - obstacleGrid [ 0 ][ w ])
for h in range ( 1 , H ):
for w in range ( 1 , W ):
obstacleGrid [ h ][ w ] = ( obstacleGrid [ h - 1 ][ w ] + obstacleGrid [ h ][ w - 1 ]) * ( 1 - obstacleGrid [ h ][ w ])
return obstacleGrid [ H - 1 ][ W - 1 ]
18: Subsets 全探索
答え 再帰で書く:$n$個の数字から得られるすべての部分配列は,$n-1$個の数字から得られるすべての部分配列のそれぞれに$n$個目の数字を入れるか入れないかで計算できる 1
2
3
4
5
6
7
8
class Solution :
def subsets ( self , nums : List [ int ]) -> List [ List [ int ]]:
def _recurse ( nums ):
if len ( nums ) == 0 :
return [[]]
sub = _recurse ( nums [ 1 :])
return sub + [ s + [ nums [ 0 ]] for s in sub ]
return _recurse ( nums )
1
2
3
4
5
6
7
8
9
10
class Solution :
def subsets ( self , nums : List [ int ]) -> List [ List [ int ]]:
ans = []
for i in range ( 1 << len ( nums )):
sub = []
for j in range ( len ( nums )):
if i & 1 << j :
sub . append ( nums [ j ])
ans . append ( sub )
return ans
1
2
3
4
5
6
class Solution :
def subsets ( self , nums : List [ int ]) -> List [ List [ int ]]:
ans = [[]]
for num in nums :
ans += [[ num ] + sub for sub in ans ]
return ans
19: Remove Duplicates from Sorted List II 一つずつ見ていく.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution :
def deleteDuplicates ( self , head : ListNode ) -> ListNode :
dummy_head = ListNode ( val =- 101 , next = head )
prev = dummy_head
current = head
while current is not None and current . next is not None :
while current . val != current . next . val :
current = current . next
prev = prev . next
if current . next is None :
return dummy_head . next
while current is not None and current . next is not None and current . val == current . next . val :
current = current . next
prev . next = current . next
current = current . next
if current is None :
return dummy_head . next
return dummy_head . next
20: Remove Duplicates from Sorted List 一個飛ばし
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution :
def deleteDuplicates ( self , head : ListNode ) -> ListNode :
current = head
while current is not None and current . next is not None :
if current . val == current . next . val :
current . next = current . next . next
else :
current = current . next
return head
21: Validate Binary Search Tree inorder で頂点に訪問したときに昇順になっていれば正しい二分探索木
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def isValidBST ( self , root : TreeNode ) -> bool :
inordered = []
def _inorder_traversal ( root ):
if root is None :
return
if root . left is not None :
_inorder_traversal ( root . left )
inordered . append ( root . val )
if root . right is not None :
_inorder_traversal ( root . right )
_inorder_traversal ( root )
for i in range ( 0 , len ( inordered ) - 1 , 1 ):
if inordered [ i ] >= inordered [ i + 1 ]:
return False
return True
左の部分木の最大値 < このノードの値 < 右の部分木の最小値を再帰的に確かめる方法もある.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def isValidBST ( self , root : TreeNode ) -> bool :
def _isValidBST ( root , larger_than , less_than ):
if root is None :
return True
if root . val <= larger_than or less_than <= root . val :
return False
return _isValidBST ( root . left , larger_than , min ( less_than , root . val )) and _isValidBST ( root . right , max ( larger_than , root . val ), less_than )
return _isValidBST ( root , float ( '-inf' ), float ( 'inf' ))
22: Binary Tree Level Order Traversal 答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def levelOrder ( self , root : TreeNode ) -> List [ List [ int ]]:
def _levelOrder ( root , lsts , level ):
if root is None :
return
lst = None
if len ( lsts ) == level :
lst = list ()
lsts . append ( lst )
else :
lst = lsts [ level ]
lst . append ( root . val )
_levelOrder ( root . left , lsts , level + 1 )
_levelOrder ( root . right , lsts , level + 1 )
return lsts
return _levelOrder ( root , [], 0 )
BFS っぽくもできる.suspendedにlevel段目の頂点のみが全部入っているように更新する.suspendedに追加しながら次の頂点に行かないようにする.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def levelOrder ( self , root : TreeNode ) -> List [ List [ int ]]:
if root is None :
return []
suspended = []
suspended . append ( root )
lsts = []
level = 0
while len ( suspended ) != 0 :
if len ( lsts ) == level :
lsts . append ([])
next_suspended = []
for u in suspended :
lsts [ level ] . append ( u . val )
if u . left is not None :
next_suspended . append ( u . left )
if u . right is not None :
next_suspended . append ( u . right )
suspended = next_suspended
level += 1
return lsts
23: Binary Tree Zigzag Level Order Traversal 一つ前のをちょっとだけイジる.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def zigzagLevelOrder ( self , root : TreeNode ) -> List [ List [ int ]]:
if root is None :
return []
suspended = []
suspended . append ( root )
lsts = []
level = 0
order_flag = - 1
while len ( suspended ) != 0 :
if len ( lsts ) == level :
lsts . append ([])
next_suspended = []
for u in suspended :
lsts [ level ] . append ( u . val )
if u . right is not None :
next_suspended . append ( u . right )
if u . left is not None :
next_suspended . append ( u . left )
suspended = next_suspended
lsts [ level ] = lsts [ level ][:: order_flag ]
order_flag = - order_flag
level += 1
return lsts
24: Maximum Depth of Binary Tree 木の深さは葉ノードから戻ってきながら計算する.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def maxDepth ( self , root : TreeNode ) -> int :
def _recurse ( root ):
if root is None :
return 0
if root . left is not None and root . right is not None :
return max ( _recurse ( root . left ), _recurse ( root . right )) + 1
if root . left is None and root . right is not None :
return _recurse ( root . right ) + 1
if root . left is not None and root . right is None :
return _recurse ( root . left ) + 1
return 1
return _recurse ( root )
25: Construct Binary Tree from Preorder and Inorder Traversal preorderからinorderを左右に分割できる.これを繰り返す.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def buildTree ( self , preorder : List [ int ], inorder : List [ int ]) -> TreeNode :
if len ( inorder ) != 0 :
idx = inorder . index ( preorder . pop ( 0 ))
root = TreeNode ( val = inorder [ idx ])
root . left = self . buildTree ( preorder , inorder [ 0 : idx ])
root . right = self . buildTree ( preorder , inorder [ idx + 1 :])
return root
26: Convert Sorted Array to Binary Search Tree 左右の部分木の高さが同じくらいにしたいので,だいたい大きさ的に真ん中ぐらいの要素から根にする.要素がソートされているのでインデックスで真ん中辺りから根を作る.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def sortedArrayToBST ( self , nums : List [ int ]) -> TreeNode :
def _recurse ( nums , low , high ):
if high < low :
return None
middle = ( low + high ) // 2
root = TreeNode ( val = nums [ middle ])
root . left = _recurse ( nums , low , middle - 1 )
root . right = _recurse ( nums , middle + 1 , high )
return root
return _recurse ( nums , 0 , len ( nums ) - 1 )
27: Minimum Depth of Binary Tree 答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def minDepth ( self , root : TreeNode ) -> int :
def _recurse ( root ):
if root is None :
return 0
if root . left is not None and root . right is not None :
return min ( _recurse ( root . left ), _recurse ( root . right )) + 1
if root . left is None :
return _recurse ( root . right ) + 1
if root . right is None :
return _recurse ( root . left ) + 1
return 1
return _recurse ( root )
28: Path Sum 全探索
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def hasPathSum ( self , root : TreeNode , targetSum : int ) -> bool :
results = []
def _recurse ( root , remaining ):
if root is None :
return
if root . left is None and root . right is None and root . val == remaining :
results . append ( True )
return
remaining -= root . val
_recurse ( root . left , remaining )
_recurse ( root . right , remaining )
_recurse ( root , targetSum )
return any ( results )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def hasPathSum ( self , root : TreeNode , targetSum : int ) -> bool :
if root is None :
return False
suspended = list ()
suspended . append (( root , root . val ))
while len ( suspended ) != 0 :
u , sofar = suspended . pop ()
if u . left is None and u . right is None and sofar == targetSum :
return True
if u . left is not None :
suspended . append (( u . left , sofar + u . left . val ))
if u . right is not None :
suspended . append (( u . right , sofar + u . right . val ))
return False
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def hasPathSum ( self , root : TreeNode , targetSum : int ) -> bool :
if root is None :
return False
suspended = list ()
suspended . append (( root , root . val ))
while len ( suspended ) != 0 :
u , sofar = suspended . pop ( 0 )
if u . left is None and u . right is None and sofar == targetSum :
return True
if u . left is not None :
suspended . append (( u . left , sofar + u . left . val ))
if u . right is not None :
suspended . append (( u . right , sofar + u . right . val ))
return False
29: Best Time to Buy and Sell Stock 最小の日を保存しながら舐める.
答え 1
2
3
4
5
6
7
8
class Solution :
def maxProfit ( self , prices : List [ int ]) -> int :
profit = 0
min_sofar = prices [ 0 ]
for i in range ( 1 , len ( prices ), 1 ):
profit = max ( profit , prices [ i ] - min_sofar )
min_sofar = min ( min_sofar , prices [ i ])
return profit
問題をちょっとだけ弄って,前日からの値段の差を格納した配列が渡されて利益の最大値を求めようとすると,これは最大部分配列和問題.
Kadane アルゴリズムで解ける.Kadane アルゴリズムは全探索の順序を替えることで前日までの最大利益を使って当日までの最大利益を低数時間で計算できて,全体として$O(n)$になるというやつ.DP.
1
2
3
4
5
6
7
8
9
class Solution :
def maxProfit ( self , priceDiff : List [ int ]) -> int :
max_profit = 0
max_current = 0
for i in range ( 1 , len ( priceDiff ), 1 ):
max_current += ( priceDiff [ i ] - priceDiff [ i - 1 ])
max_current = max ( 0 , max_current )
max_profit = max ( max_profit , max_current )
return max_profit
30: Best Time to Buy and Sell Stock II 今日より明日のほうが高値なら,今日買って明日売ろう.
答え 1
2
3
class Solution :
def maxProfit ( self , prices : List [ int ]) -> int :
return sum ( max ( 0 , prices [ i + 1 ] - prices [ i ]) for i in range ( len ( prices ) - 1 ))
31: Word Ladder グリッドグラフの文字列版だと思えれば大丈夫.グリッドグラフのマス目に 1 文字だけ違う文字列を書き込んでグラフ上のマス目を踏んでいくイメージ.言うなれば 26 次元グリッドグラフか.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution :
def ladderLength ( self , beginWord : str , endWord : str , wordList : List [ str ]) -> int :
not_visited_yet = set ( wordList )
suspended = list ()
not_visited_yet . add ( beginWord )
suspended . append (( beginWord , 1 ))
while len ( suspended ) != 0 :
word , length = suspended . pop ( 0 )
if word == endWord :
return length
for i in range ( len ( word )):
for char in 'abcdefghijklmnopqrstuvwxyz' :
next_candidate = word [: i ] + char + word [ i + 1 :]
if next_candidate in not_visited_yet :
not_visited_yet . remove ( next_candidate )
suspended . append (( next_candidate , length + 1 ))
return 0
32: Word Break wordDict内の文字列の重複を許す組み合わせを全部求めてsと一致するかを調べても$O(2^n)$で原理的には解けるが1 <= len(wordDict) <= 1000なので間に合わない.
そこでsについて考える.「$i$文字目より前の部分文字列s[:i]を実現できるか」は「$j$($j < i$)文字目より前の部分文字列s[:j]を実現できて,かつ残りのs[j:i]がwordDict内にあるか」で求まる.DP.
答え 1
2
3
4
5
6
7
8
class Solution :
def wordBreak ( self , s : str , wordDict : List [ str ]) -> bool :
# dp[i]: whether s[:i] can be build from words in wordDict
words = set ( wordDict ) # for lookup in O(1)
dp = [ True ]
for i in range ( 1 , len ( s ) + 1 ):
dp += [ any ( dp [ j ] and s [ j : i ] in words for j in range ( i ))]
return dp [ len ( s )]
「wordDict内にある最長の文字列の長さ」以上のs部分文字列がwordDict内にあるはずがないのでそれを省くと効率が良くなる.
1
2
3
4
5
6
7
8
9
class Solution :
def wordBreak ( self , s : str , wordDict : List [ str ]) -> bool :
# dp[i]: whether s[:i] can be build from words in wordDict
words = set ( wordDict ) # for lookup in O(1)
max_len = max ( map ( len , wordDict ))
dp = [ True ]
for i in range ( 1 , len ( s ) + 1 ):
dp += [ any ( dp [ j ] and s [ j : i ] in words for j in range ( max ( 0 , i - max_len ), i ))]
return dp [ len ( s )]
33: Linked List Cycle 二人走らせる.出逢えばループあり.足の早いほうが崖から落ちればループなし.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution :
def hasCycle ( self , head : ListNode ) -> bool :
if head is None :
return False
slower = head
faster = head
while faster . next is not None and faster . next . next is not None :
slower = slower . next
faster = faster . next . next
if slower is faster :
return True
return False
34: Linked List Cycle II 二人走らせる.1 周回差つけられたところで初めて出会う.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution :
def detectCycle ( self , head : ListNode ) -> ListNode :
if head is None :
return None
faster = head
slower = head
has_loop = False
while faster . next is not None and faster . next . next is not None :
slower = slower . next
faster = faster . next . next
if slower is faster :
has_loop = True
slower = head
break
if has_loop :
while slower is not faster :
slower = slower . next
faster = faster . next
return slower
else :
return None
35: Find Minimum in Rotated Sorted Array 二分探索っぽいことをする.昇順になったものを回転させるときの折れ線グラフを描く真ん中と左右の比較でどこに最小値があるかがわかる.
答え 1
2
3
4
5
6
7
8
9
10
class Solution :
def findMin ( self , nums : List [ int ]) -> int :
left , right = 0 , len ( nums ) - 1
while left < right :
middle = ( left + right ) // 2
if nums [ middle ] < nums [ right ]:
right = middle
else :
left = middle + 1
return nums [ left ]
元の配列が昇順に並んであるので「先頭要素より小さくなる最小のインデックスの位置にある要素がほしい」と問題を言い換えられれば,めぐる式二分探索に落とし込める.
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution :
def findMin ( self , nums : List [ int ]) -> int :
def is_ok ( mid ):
return nums [ mid ] < nums [ 0 ]
ng = - 1
ok = len ( nums )
while 1 < abs ( ok - ng ):
mid = ( ok + ng ) // 2
if is_ok ( mid ):
ok = mid
else :
ng = mid
return nums [ ok ] if ok != len ( nums ) else nums [ 0 ]
36: House Robber [2,1,1,2]というパターンを忘れてはならない.
答え dp[i]:i番目までの家から盗めるお金の最大値
dp[i] = max(dp[i-2] + nums[i], dp[i-1])
1
2
3
4
5
6
7
8
9
10
11
12
class Solution :
def rob ( self , nums : List [ int ]) -> int :
# dp[i]: nums[:i+1]での盗めるお金の最大値
# dp[i] = max(dp[i-1], dp[i-2] + nums[i])
if len ( nums ) < 3 :
return max ( nums )
dp = [ 0 ] * len ( nums )
dp [ 0 ] = nums [ 0 ]
dp [ 1 ] = max ( nums [ 0 ], nums [ 1 ])
for i in range ( 2 , len ( nums )):
dp [ i ] = max ( dp [ i - 1 ], dp [ i - 2 ] + nums [ i ])
return dp [ - 1 ]
37: Number of Islands グリッドグラフの全探索.拙著記事はここ .
答え queue を使う BFS の答え
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution :
def numIslands ( self , grid : List [ List [ str ]]) -> int :
dirs = [( 1 , 0 ), ( - 1 , 0 ), ( 0 , 1 ), ( 0 , - 1 )]
H = len ( grid )
W = len ( grid [ 0 ])
has_visited = set ()
suspended = list ()
ans = 0
for h in range ( H ):
for w in range ( W ):
if ( h , w ) in has_visited or grid [ h ][ w ] == "0" :
continue
has_visited . add (( h , w ))
suspended . append (( h , w ))
ans += 1
while len ( suspended ) != 0 :
( _h , _w ) = suspended . pop ( 0 )
for ( dh , dw ) in dirs :
next_h = _h + dh
next_w = _w + dw
if 0 <= next_h < H and 0 <= next_w < W and grid [ next_h ][ next_w ] == "1" and ( next_h , next_w ) not in has_visited :
has_visited . add (( next_h , next_w ))
suspended . append (( next_h , next_w ))
return ans
stack を使う DFS の答え
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution :
def numIslands ( self , grid : List [ List [ str ]]) -> int :
dirs = [( 1 , 0 ), ( - 1 , 0 ), ( 0 , 1 ), ( 0 , - 1 )]
H = len ( grid )
W = len ( grid [ 0 ])
has_visited = set ()
suspended = list ()
ans = 0
for h in range ( H ):
for w in range ( W ):
if ( h , w ) in has_visited or grid [ h ][ w ] == "0" :
continue
has_visited . add (( h , w ))
suspended . append (( h , w ))
ans += 1
while len ( suspended ) != 0 :
( _h , _w ) = suspended . pop ()
for ( dh , dw ) in dirs :
next_h = _h + dh
next_w = _w + dw
if 0 <= next_h < H and 0 <= next_w < W and grid [ next_h ][ next_w ] == "1" and ( next_h , next_w ) not in has_visited :
has_visited . add (( next_h , next_w ))
suspended . append (( next_h , next_w ))
return ans
再気をつかう DFS の答え
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution :
def numIslands ( self , grid : List [ List [ str ]]) -> int :
dirs = [( 1 , 0 ), ( - 1 , 0 ), ( 0 , 1 ), ( 0 , - 1 )]
H = len ( grid )
W = len ( grid [ 0 ])
has_visited = set ()
ans = 0
def dfs ( h , w ):
has_visited . add (( h , w ))
for ( dh , dw ) in dirs :
nh = h + dh
nw = w + dw
if 0 <= nh < H and 0 <= nw < W and grid [ nh ][ nw ] == "1" and ( nh , nw ) not in has_visited :
dfs ( h + dh , w + dw )
for h in range ( H ):
for w in range ( W ):
if ( h , w ) in has_visited or grid [ h ][ w ] == "0" :
continue
ans += 1
dfs ( h , w )
return ans
38: Reverse Linked List 答え 遅い.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution :
def reverseList ( self , head : ListNode ) -> ListNode :
if head is None :
return None
if head . next is None :
return ListNode ( val = head . val )
reversed_head = self . reverseList ( head . next )
reversed_tail = reversed_head
while reversed_tail . next is not None :
reversed_tail = reversed_tail . next
reversed_tail . next = ListNode ( val = head . val )
return reversed_head
賢く.
1
2
3
4
5
6
7
8
9
10
11
12
13
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution :
def reverseList ( self , head : ListNode ) -> ListNode :
if head is None or head . next is None :
return head
reversed_head = self . reverseList ( head . next )
head . next . next = head
head . next = None
return reversed_head
繰り返しで.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution :
def reverseList ( self , head : ListNode ) -> ListNode :
prev = None
curr = head
while curr is not None :
tmp = curr . next
curr . next = prev
prev = curr
curr = tmp
return prev
39: Minimum Size Subarray Sum 答え 力技なら部分列を全部取って計算するので$O(n^3)$で間に合わない.
累積和を使って部分列の和を$O(1)$で求めて全体で$O(n^2)$.ただこれだと Python だと間に合わない.
1
2
3
4
5
6
7
8
9
10
11
12
class Solution :
def minSubArrayLen ( self , target : int , nums : List [ int ]) -> int :
accum = [ nums [ 0 ]]
for num in nums [ 1 :]:
accum . append ( accum [ - 1 ] + num )
ans = 10 ** 9
for i in range ( 0 , len ( nums ), 1 ):
for j in range ( i , len ( nums ), 1 ):
added = accum [ j ] - accum [ i ] + nums [ i ]
if target <= added :
ans = min ( ans , ( j - i + 1 ))
return ans if ans != 10 ** 9 else 0
部分和の大きさについて,部分列の長さが長くなればなるほど部分和は単調に増加するので,target以上となる最小のインデックスは二分探索で探せる.全体としては$O(n \log n)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution :
def minSubArrayLen ( self , target : int , nums : List [ int ]) -> int :
accum = [ nums [ 0 ]]
for num in nums [ 1 :]:
accum . append ( accum [ - 1 ] + num )
def is_ok ( lst , mid , key ):
if key <= lst [ mid ]:
return True
return False
def binary_search ( lst , key ):
ng = - 1
ok = len ( lst )
while 1 < abs ( ok - ng ):
mid = ( ok + ng ) // 2
if is_ok ( lst , mid , key ):
ok = mid
else :
ng = mid
return ok
ans = 10 ** 9
for i in range ( 0 , len ( nums ), 1 ):
accum_j = target + accum [ i ] - nums [ i ]
j = binary_search ( accum [ i :], accum_j ) + i
if j == len ( accum ):
continue
ans = min ( ans , ( j - i + 1 ))
return ans if ans != 10 ** 9 else 0
もっと賢いやり方がある.部分列の和は,「部分列が長ければ長いほど大きくなる」ので,一度部分列の和がtarget以上になったらそれ以上その部分列を伸ばして探しても答えに関係ない.部分列の末端の位置が早々に確定できるので,部分列の先頭を回すだけで求まる.$O(n)$.これは世の中では尺取法と呼ばれているそうだ.英語では sliding window と呼ばれているのか?
1
2
3
4
5
6
7
8
9
10
11
12
class Solution :
def minSubArrayLen ( self , target : int , nums : List [ int ]) -> int :
ans = float ( "inf" )
left = 0
accum = 0
for right in range ( len ( nums )):
accum += nums [ right ]
while target <= accum :
ans = min ( ans , right - left + 1 )
accum -= nums [ left ]
left += 1
return ans if ans != float ( "inf" ) else 0
40: House Robber II 答え nums[0]とnums[-1]を同時に襲えないので,nums[1:]を対象にしたときとnums[:-1]を対象にしたときを別個に計算して大きい方を取ればいい.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution :
def rob ( self , nums : List [ int ]) -> int :
if len ( nums ) < 3 :
return max ( nums )
def _rob ( nums ):
# dp[i]: nums[:i+1]までで盗めるお金の最大値
if len ( nums ) < 3 :
return max ( nums )
dp = [ 0 ] * len ( nums )
dp [ 0 ] = nums [ 0 ]
dp [ 1 ] = max ( nums [ 0 ], nums [ 1 ])
for i in range ( 2 , len ( nums )):
dp [ i ] = max ( dp [ i - 1 ], dp [ i - 2 ] + nums [ i ])
return dp [ len ( nums ) - 1 ]
return max ( _rob ( nums [ 1 :]), _rob ( nums [: len ( nums ) - 1 ]))
41: Meeting Rooms 複数の MTG の開始時刻と終了時刻が与えられるとき,全ての MTG 予定がダブらないかどうかを判定せよ.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
# Definition for an interval
# class Interval(object):
# def __init__(self, s=0, e=0):
# self.start = s
# self.end = e
class Solution :
def canAttendMeetings ( self , intervals : List [ Interval ]) -> bool :
intervals . sort ( key = lambda x : x . start )
for i in range ( 0 , len ( intervals ) - 1 , 1 ):
if intervals [ i ] . end > intervals [ i + 1 ] . start :
return False
return True
42: Meeting Rooms II 複数の MTG の開始時刻と終了時刻が与えられるとき,必要最小限の MTG 部屋の数を計算せよ.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Definition for an interval
# class Interval(object):
# def __init__(self, s=0, e=0):
# self.start = s
# self.end = e
class Solution :
def minMeetingRooms ( self , intervals : List [ Interval ]) -> int :
intervals . sort ( key = lambda x : x . start )
heap = []
for mtg in intervals :
if len ( heap ) != 0 and heap [ 0 ] <= mtg . start :
heapq . heappop ( heap )
heapq . heappush ( heap , mtg . end )
else :
heapq . heappush ( heap , mtg . end )
return len ( heap )
43: Paint Fence $N$本の柱を$K$色で塗り分ける.このとき,連続して同じ色の柱は$2$本より多くなってはならない.塗り分け方の総数を求めよ.
答え 柱を左から右に塗っていくことを考える.左からpos - 2,pos - 1,posの位置にある柱の色の塗り方は
「pos - 2,pos - 1が連続して同じ色 X,posが X 以外」でposに使える色は$K - 1$色 「pos - 2が色 X,pos - 1,posが連続して X 以外の色」でposに使える色は$K - 1$色 1
2
3
4
5
6
7
8
9
10
11
class Solution :
def numWays ( self , n : int , k : int ) -> int :
if n == 1 :
return k
if n == 2 :
reteurn k ** 2
# dp[i]: 左からi番目までの柱の塗り分け方
dp = [ 0 , k , k ** 2 ]
for i in range ( 2 , n ):
dp += [( dp [ - 2 ] + dp [ - 1 ]) * ( k - 1 )]
return dp [ n ]
44: Move Zeroes 答え 1
2
3
4
5
6
7
8
9
10
class Solution :
def moveZeroes ( self , nums : List [ int ]) -> None :
"""
Do not return anything, modify nums in-place instead.
"""
last_non_zero_at = 0
for i in range ( 0 , len ( nums ), 1 ):
if nums [ i ] != 0 :
nums [ last_non_zero_at ], nums [ i ] = nums [ i ], nums [ last_non_zero_at ]
last_non_zero_at += 1
非$0$要素の数をカウントというやり方でもいい.
1
2
3
4
5
6
7
8
9
10
11
12
class Solution :
def moveZeroes ( self , nums : List [ int ]) -> None :
"""
Do not return anything, modify nums in-place instead.
"""
non_zero = 0
for num in nums :
if num != 0 :
nums [ non_zero ] = num
non_zero += 1
for i in range ( non_zero , len ( nums )):
nums [ i ] = 0
45: Longest Increasing Subsequence 答え 力技でやるなら全ての部分列を取り上げて長さの最小値を求める.$O(2^n)$.
再帰を使って全探索.当然 TLE.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution :
def lengthOfLIS ( self , nums : List [ int ]) -> int :
def check ( seq ):
for i in range ( 0 , len ( seq ) - 1 , 1 ):
if seq [ i ] >= seq [ i + 1 ]:
return False
return True
lens = []
def _recurse ( pos , seq ):
if pos == len ( nums ):
if check ( seq ):
lens . append ( len ( seq ))
return
_recurse ( pos + 1 , seq )
_recurse ( pos + 1 , seq + [ nums [ pos ]])
_recurse ( 0 , [])
return max ( lens )
bit 全探索.これも当然 TLE.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution :
def lengthOfLIS ( self , nums : List [ int ]) -> int :
def check ( seq ):
for i in range ( 0 , len ( seq ) - 1 , 1 ):
if seq [ i ] >= seq [ i + 1 ]:
return False
return True
ans = 0
for i in range ( 1 << len ( nums )):
seq = []
for j in range ( len ( nums )):
if i & ( 1 << j ):
seq . append ( nums [ j ])
if check ( seq ):
ans = max ( ans , len ( seq ))
return ans
DP で解くと$O(n^2)$
dp[i]:nums[i]で終わる最長部分増加列の長さ
dp[i]はdp[0],dp[1],dp[2],…dp[i-1]を使って計算できる.dp[i]は「nums[i]がnums[j]以上であるようなjの中での最大のdp[j]に 1 足したもの」
1
2
3
for j in range ( 0 , i ):
if nums [ j ] < nums [ i ]:
dp [ i ] = max ( dp [ i ], dp [ j ] + 1 )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution :
def lengthOfLIS ( self , nums : List [ int ]) -> int :
# dp[i]: nums[i]で終わる最大増加部分列の長さ
# dp[i] = {
# nums[j] < nums[i]を満たすようなj(0 < j < i)に対して
# 最大のdp[j] + 1
# }
dp = [ 0 for _ in range ( len ( nums ))]
for i in range ( len ( nums )):
dp [ i ] = 1 # 長さ1の増加部分列:[nums[i]]
for j in range ( i ):
if nums [ j ] < nums [ i ]:
dp [ i ] = max ( dp [ i ], dp [ j ] + 1 )
return max ( dp )
添字を逆転させた DP を考えると$O(n \log n)$で解ける.
dp[i]:長さi + 1の増加部分列の右端要素の最小値
全ての部分列を取り出してdpを埋めたあとのことを考えると,dpは単調に増加するような数列になっているはず.これは別に全ての部分列を列挙し終わってからでなくても,要素を一つずつ見て最適なdpの位置に置くことでも得ることができる.つまり,要素を一つずつ見ながら,二分探索でその要素が入る位置を求めてdpを求めることができる.
1
2
3
4
5
6
7
class Solution :
def lengthOfLIS ( self , nums : List [ int ]) -> int :
# dp[i]: minimum of the last element of an increasing subsequence which length is i+1
dp = [ float ( "inf" )] * len ( nums )
for num in nums :
dp [ bisect_left ( dp , num )] = num
return bisect_left ( dp , float ( "inf" ))
二分探索を自分で実装したらこう.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution :
def lengthOfLIS ( self , nums : List [ int ]) -> int :
# dp[i]: 長さi+1の増加部分列の終端要素の最小値
dp = [ float ( "inf" )] * len ( nums )
def binary_search ( nums , key ):
ok = len ( nums )
ng = - 1
def is_ok ( mid ):
return key <= nums [ mid ]
while 1 < abs ( ng - ok ):
mid = ( ng + ok ) // 2
if is_ok ( mid ):
ok = mid
else :
ng = mid
return ok
for num in nums :
dp [ binary_search ( dp , num )] = num
return binary_search ( dp , float ( "inf" ))
46: Coin Change 答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution :
def coinChange ( self , coins : List [ int ], amount : int ) -> int :
# dp[i][j]: i番目までのコインを使ってj円を実現するときの最小枚数
# dp[i][j] = min(dp[i-1][j], dp[i][j-coins[i]] + 1)
coins = [ - 1 ] + coins
INF = 10 ** 9
dp = [[ INF for _ in range ( amount + 1 )] for _ in range ( len ( coins ))]
for i in range ( len ( coins )):
dp [ i ][ 0 ] = 0
for i in range ( 1 , len ( coins )):
for j in range ( amount + 1 ):
if 0 <= j - coins [ i ]:
dp [ i ][ j ] = min ( dp [ i - 1 ][ j ], dp [ i ][ j - coins [ i ]] + 1 )
else :
dp [ i ][ j ] = dp [ i - 1 ][ j ]
return dp [ - 1 ][ - 1 ] if dp [ - 1 ][ - 1 ] != INF else - 1
DP 配列は二次元でなくても大丈夫だった.
1
2
3
4
5
6
7
8
class Solution :
def coinChange ( self , coins : List [ int ], amount : int ) -> int :
# dp[i]: i円支払うときの最小枚数
dp = [ float ( 'inf' ) for _ in range ( amount + 1 )]
dp [ 0 ] = 0
for i in range ( 1 , amount + 1 ):
dp [ i ] = min ([ dp [ i - coin ] if 0 <= i - coin else float ( 'inf' ) for coin in coins ]) + 1
return dp [ amount ] if dp [ amount ] != float ( 'inf' ) else - 1
47: Number of Connected Components in an Undirected Graph 答え 問題文が見れないので標準入力経由でグラフを入力されたと想定して解く.ある頂点から始める DFS を.未訪問の頂点がなくなるまで繰り返す.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# graph:
# 0
# / | \
# 1--2 3
# | \
# 4 6
# 5--7
N , M = map ( int , input () . split ())
G = [[] for _ in range ( N )]
for _ in range ( M ):
u , v = map ( int , input () . split ())
G [ u ] . append ( v )
G [ v ] . append ( u )
def connected_component ( graph ):
cc = 0
has_visited = set ()
for n in range ( len ( graph )):
if n not in has_visited :
cc += 1
suspended = [ n ]
while len ( suspended ) != 0 :
u = suspended . pop ()
if u in has_visited :
continue
has_visited . add ( u )
for v in graph [ u ]:
suspended . append ( v )
return cc
print ( connected_component ( G ))
48: Top K Frequent Elements 大きい順に$K$個,小さい順に$K$個は色々やり方がある.拙著はこちら
答え 素直に書いても通る.
1
2
3
4
5
6
7
8
9
10
11
class Solution :
def topKFrequent ( self , nums : List [ int ], k : int ) -> List [ int ]:
table = dict ()
for num in nums :
if num in table :
table [ num ] += 1
else :
table [ num ] = 0
ordered = list ( table . items ())
ordered . sort ( key = lambda x : x [ 1 ], reverse = True )
return [ x [ 0 ] for x in ordered [: k ]]
heapq.nlargestを使う.
1
2
3
4
class Solution :
def topKFrequent ( self , nums : List [ int ], k : int ) -> List [ int ]:
cnt = [( freq , num ) for num , freq in Counter ( nums ) . items ()]
return [ num for _ , num in heapq . nlargest ( k , cnt )]
この問題 が復習になる.
49: Intersection of Two Arrays python が偉い.
答え 1
2
3
class Solution :
def intersection ( self , nums1 : List [ int ], nums2 : List [ int ]) -> List [ int ]:
return list ( set ( nums1 ) . intersection ( set ( nums2 )))
50: Find K Pairs with Smallest Sums 答え 力技 1:テーブル全部計算する.
1
2
3
class Solution :
def kSmallestPairs ( self , nums1 : List [ int ], nums2 : List [ int ], k : int ) -> List [ List [ int ]]:
return sorted ( itertools . product ( nums1 , nums2 ), key = sum )[: k ]
力技 2:テーブル全部計算する.
1
2
3
class Solution :
def kSmallestPairs ( self , nums1 : List [ int ], nums2 : List [ int ], k : int ) -> List [ List [ int ]]:
return map ( list , sorted ( itertools . product ( nums1 , nums2 ), key = sum )[: k ])
力技 3:generator を使って必要な分だけ計算する.
1
2
3
class Solution :
def kSmallestPairs ( self , nums1 : List [ int ], nums2 : List [ int ], k : int ) -> List [ List [ int ]]:
return map ( list , heapq . nsmallest ( k , itertools . product ( nums1 , nums2 ), key = sum ))
力技 4:これも generator
1
2
3
class Solution :
def kSmallestPairs ( self , nums1 : List [ int ], nums2 : List [ int ], k : int ) -> List [ List [ int ]]:
return heapq . nsmallest ( k , ([ u , v ] for u in nums1 for v in nums2 ), key = sum )
テーブルを 1 行ごと計算する generator
1
2
3
4
5
class Solution :
def kSmallestPairs ( self , nums1 : List [ int ], nums2 : List [ int ], k : int ) -> List [ List [ int ]]:
streams = map ( lambda u : ([ u + v , u , v ] for v in nums2 ), nums1 )
stream = heapq . merge ( * streams )
return [ ret [ 1 :] for ret in itertools . islice ( stream , k )]
テーブルの左端の方だけ欲しいというのを優先度付きキューを使ってうまく実装する.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution :
def kSmallestPairs ( self , nums1 : List [ int ], nums2 : List [ int ], k : int ) -> List [ List [ int ]]:
queue = []
def push ( i , j ):
if i < len ( nums1 ) and j < len ( nums2 ):
heapq . heappush ( queue , [ nums1 [ i ] + nums2 [ j ], i , j ])
push ( 0 , 0 )
ans = []
while len ( queue ) != 0 and len ( ans ) < k :
_ , i , j = heapq . heappop ( queue )
ans . append ([ nums1 [ i ], nums2 [ j ]])
push ( i , j + 1 )
if j == 0 :
push ( i + 1 , j )
return ans
51: First Unique Character in a String 答え 1
2
3
4
5
6
7
8
class Solution :
def firstUniqChar ( self , s : str ) -> int :
for idx , char in enumerate ( s ):
if char in s [: idx ] + s [ idx + 1 :]:
continue
else :
return idx
return - 1
52: Is Subsequence iter化することで,見つかるまで文字を吐き出すイテレータを作る.
答え 1
2
3
4
5
6
7
class Solution :
def isSubsequence ( self , s : str , t : str ) -> bool :
t = iter ( t )
for ch in s :
if ch not in t :
return False
return True
1
2
3
4
class Solution :
def isSubsequence ( self , s : str , t : str ) -> bool :
t = iter ( t )
return all ( char in t for char in s )
53: Subarray Sum Equals K 答え 力技.$O(n^3)$.TLE.
1
2
3
4
5
6
7
8
9
10
11
class Solution :
def subarraySum ( self , nums : List [ int ], k : int ) -> int :
ans = 0
for start in range ( len ( nums )):
for end in range ( start + 1 , len ( nums ) + 1 ):
subsum = 0
for num in nums [ start : end ]:
subsum += num
if subsum == k :
ans += 1
return ans
累積和を使ってsubsumを求めて$O(n^2)$.TLE.
1
2
3
4
5
6
7
8
9
10
11
12
class Solution :
def subarraySum ( self , nums : List [ int ], k : int ) -> int :
ans = 0
accum = [ 0 ]
for num in nums :
accum += [ accum [ - 1 ] + num ]
for start in range ( len ( nums )):
for end in range ( start + 1 , len ( nums ) + 1 ):
subsum = accum [ end ] - accum [ start ]
if subsum == k :
ans += 1
return ans
subsumを求めながら添え字を回す.$O(n^2)$.TLE.
1
2
3
4
5
6
7
8
9
10
class Solution :
def subarraySum ( self , nums : List [ int ], k : int ) -> int :
ans = 0
for start in range ( len ( nums )):
subsum = 0
for end in range ( start , len ( nums )):
subsum += nums [ end ]
if subsum == k :
ans += 1
return ans
結局部分列の個数だけカウントしたいのであれば,部分列の最初と最後のインデックスはいらなくて,合計がいくらになる部分列が何個あるかが重要.
1
2
3
4
5
6
7
8
9
10
11
12
class Solution :
def subarraySum ( self , nums : List [ int ], k : int ) -> int :
ans = 0
subsum = 0
table = dict () # subsum: freq
table [ 0 ] = 1
for num in nums :
subsum += num
if subsum - k in table :
ans += table [ subsum - k ]
table [ subsum ] = table . get ( subsum , 0 ) + 1
return ans
54: Merge Two Binary Trees 答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def mergeTrees ( self , root1 : TreeNode , root2 : TreeNode ) -> TreeNode :
if root1 is None :
return root2
if root2 is None :
return root1
root1 . val += root2 . val
root1 . left = self . mergeTrees ( root1 . left , root2 . left )
root1 . right = self . mergeTrees ( root1 . right , root2 . right )
return root1
55: Max Area of Island 答え DFS で全探索.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution :
def maxAreaOfIsland ( self , grid : List [ List [ int ]]) -> int :
H = len ( grid )
W = len ( grid [ 0 ])
dirs = [( 1 , 0 ), ( - 1 , 0 ), ( 0 , 1 ), ( 0 , - 1 )]
has_visited = set ()
def traverse ( h , w ):
area = 0
suspended = list ()
suspended . append (( h , w ))
while len ( suspended ) != 0 :
h_ , w_ = suspended . pop ()
has_visited . add (( h_ , w_ ))
area += 1
for ( dh , dw ) in dirs :
nh = h_ + dh
nw = w_ + dw
if 0 <= nh < H and 0 <= nw < W and ( nh , nw ) not in has_visited and grid [ nh ][ nw ] == 1 :
has_visited . add (( nh , nw ))
suspended . append (( nh , nw ))
return area
max_area = 0
for h in range ( H ):
for w in range ( W ):
if grid [ h ][ w ] == 1 :
area = traverse ( h , w )
max_area = max ( max_area , area )
return max_area
BFS で全探索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution :
def maxAreaOfIsland ( self , grid : List [ List [ int ]]) -> int :
H = len ( grid )
W = len ( grid [ 0 ])
dirs = [( 1 , 0 ), ( - 1 , 0 ), ( 0 , 1 ), ( 0 , - 1 )]
has_visited = set ()
def traverse ( h , w ):
area = 0
suspended = list ()
suspended . append (( h , w ))
while len ( suspended ) != 0 :
h_ , w_ = suspended . pop ( 0 )
has_visited . add (( h_ , w_ ))
area += 1
for ( dh , dw ) in dirs :
nh = h_ + dh
nw = w_ + dw
if 0 <= nh < H and 0 <= nw < W and ( nh , nw ) not in has_visited and grid [ nh ][ nw ] == 1 :
has_visited . add (( nh , nw ))
suspended . append (( nh , nw ))
return area
max_area = 0
for h in range ( H ):
for w in range ( W ):
if grid [ h ][ w ] == 1 :
area = traverse ( h , w )
max_area = max ( max_area , area )
return max_area
再帰で DFS.再帰関数は地点(i, j)を端点とした土地の面積を返す.上下左右の土地はつながっていないので上下左右から始めた土地の面積の合計に 1 足せば良い.
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution :
def maxAreaOfIsland ( self , grid : List [ List [ int ]]) -> int :
H = len ( grid )
W = len ( grid [ 0 ])
dirs = [( 1 , 0 ), ( - 1 , 0 ), ( 0 , 1 ), ( 0 , - 1 )]
has_visited = set ()
def area_from ( h , w ):
if ( h < 0 or H <= h ) or ( w < 0 or W <= w ) or ( h , w ) in has_visited or grid [ h ][ w ] == 0 :
return 0
has_visited . add (( h , w ))
return 1 + sum ( area_from ( h + dh , w + dw ) for ( dh , dw ) in dirs )
return max ( area_from ( h , w ) for h in range ( H ) for w in range ( W ))
56: Kth Largest Element in a Stream 大きい方から数えて$k$番目の要素は,昇順に並ぶ長さ$k$の優先度付きキューの先頭.
答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class KthLargest :
def __init__ ( self , k : int , nums : List [ int ]):
self . queue = nums
self . k = k
heapq . heapify ( self . queue )
while k < len ( self . queue ):
heapq . heappop ( self . queue )
def add ( self , val : int ) -> int :
if len ( self . queue ) < self . k :
heapq . heappush ( self . queue , val )
elif self . queue [ 0 ] < val :
heapq . heappop ( self . queue )
heapq . heappush ( self . queue , val )
return self . queue [ 0 ]
# Your KthLargest object will be instantiated and called as such:
# obj = KthLargest(k, nums)
# param_1 = obj.add(val)
57: Split BST 答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class TreeNode :
def __init__ ( self , val = 0 , left = None , right = None ):
self . val = val
self . left = left
self . right = right
def splitBST ( root , v ):
inordered = []
def inorder_traverse ( root ):
if root is None :
return
inorder_traverse ( root . left )
inordered . append ( root . val )
inorder_traverse ( root . right )
inorder_traverse ( root )
idx = inordered . index ( v )
def build_bst ( i , j ):
if j < i :
return None
mid = ( i + j ) // 2
root = TreeNode ( inordered [ mid ])
root . left = build_bst ( i , mid - 1 )
root . right = build_bst ( mid + 1 , j )
return root
return [ build_bst ( 0 , idx ), build ( idx , len ( inordered ) - 1 )]
58: K-th Symbol in Grammar $i+1$行目のビット列$s_{i+1}$は$i$列目のビット列$s_i$とそのビット反転したものを連結したものになっている.これを使って真面目に文字列を全部求めると時間かかる.$s_{i+1}$の前半は$s_i$と同じなので,問題のサイズを半分にすることができる.
答え 1
2
3
4
5
6
7
8
9
class Solution :
def kthGrammar ( self , N : int , K : int ) -> int :
if N == 1 :
return 0
half = 1 << ( N - 2 )
if K <= half :
return self . kthGrammar ( N - 1 , K )
else :
return self . kthGrammar ( N - 1 , K - half ) ^ 1
59: Unique Email Addresses 答え 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution :
def numUniqueEmails ( self , emails : List [ str ]) -> int :
table = dict ()
for email in emails :
( local , domain ) = email . split ( "@" )
local = local . replace ( "." , "" )
idx = local . find ( "+" )
if idx == - 1 :
idx = len ( local )
local = local [: idx ]
if domain in table :
table [ domain ] . add ( local )
else :
table [ domain ] = { local }
ans = 0
for ls in table . values ():
ans += len ( list ( ls ))
return ans
+の処理を先にしたほうが効率的らしい.
1
2
3
4
5
6
7
8
class Solution :
def numUniqueEmails ( self , emails : List [ str ]) -> int :
canonicals = set ()
for email in emails :
( local , domain ) = email . split ( "@" )
local = local . split ( "+" )[ 0 ] . replace ( "." , "" )
canonicals . add ( local + "@" + domain )
return len ( canonicals )
60: Capacity To Ship Packages Within D Days 答え 無限に積める船があれば確実に$D$日以内に運べる.逆に許容積載量が$0$なら絶対に運べない.「ある条件を満たす最小値」と来れば,二分探索の出番.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution :
def shipWithinDays ( self , weights : List [ int ], D : int ) -> int :
def is_ok ( mid ):
elapsed = 1
loaded = 0
for weight in weights :
loaded += weight
if mid < loaded :
elapsed += 1
loaded = weight
return elapsed <= D
ng = max ( weights ) - 1 # 常に条件を満たさない
ok = sum ( weights ) + 1 # 常に条件を満たす
while 1 < abs ( ng - ok ):
mid = ( ng + ok ) // 2
if is_ok ( mid ):
ok = mid
else :
ng = mid
return ok