グラフ探索

# グラフを探索したい

計算機を「与えられた対象の中から，目的に合致するものを見つけ出したり，最良のものを見つけ出す」という「探索」目的で用いる場面は多くある．世の中にはびこっている問題たちは，考えられるすべての場合をくまなく調べつ尽くすことによって原理的に解決することができる．

問題を「グラフ」としてモデル化・定式化することで高速な探索アルゴリズムを考えることができることが多い．例えば，首都圏の電車の乗換案内アプリケーションはほとんどそのままグラフ上の最短経路探索問題として定式化できるし，他にもオセロや将棋などのボードゲームも，ユーザの操作によって盤上の状態を頂点とするグラフ上を移動しているとすればグラフ上の探索問題とみなせる．

# グラフ

グラフとは，対象物を構成する事物の集合とその集合を構成する対象物間の関係にのみ注目したデータ構造のことで，卑近な例で言えば，人間関係はグラフとして表現することができる．

**グラフ$G$**はそれを構成する頂点の有限集合$V = \{v_1, v_2, …, v_n\}$と頂点間に生える辺の有限集合$E = \{e_1, e_2, …, e_m\}$の組として定義される．

$$ G = (V, E) $$

頂点$v_i$と$v_j$が辺$e$によって接続されているとき，頂点$v_i$と$v_j$は互いに隣接しているといい，$v_i$，$v_j$は$e$の端点であるという．

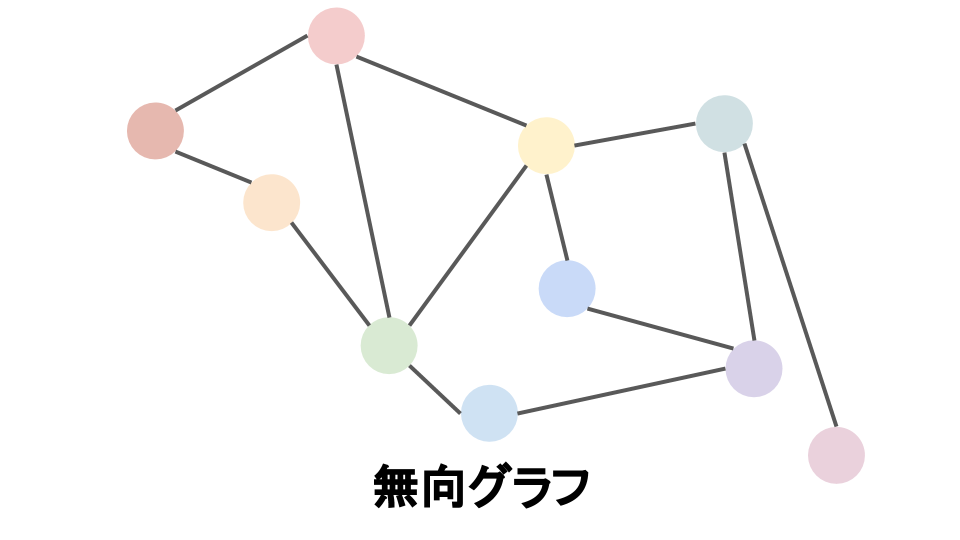
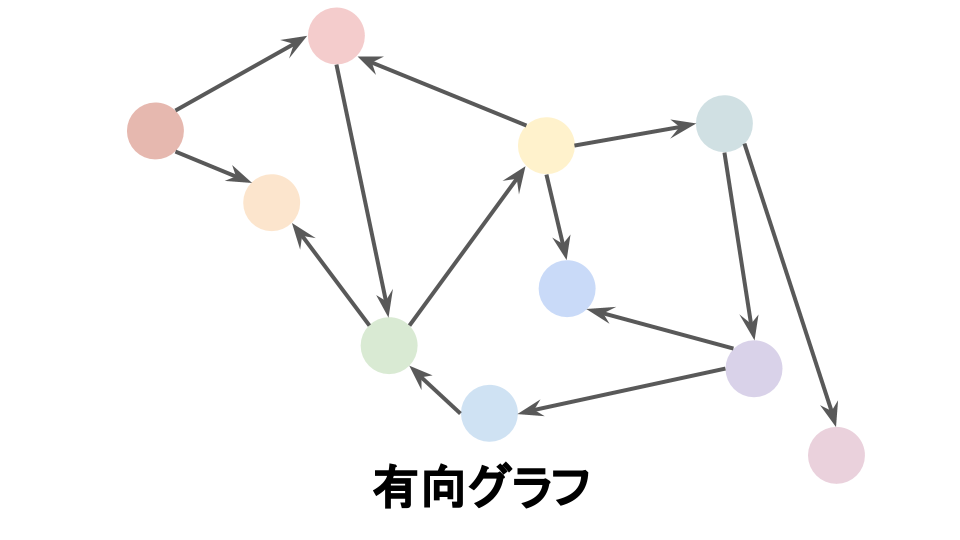
グラフ$G$の各辺$e = (v_i, v_j)$について，$(v_i, v_j)$と$(v_j, v_i)$を区別しないとき，$G$を無向グラフと呼び，逆に区別するとき有向グラフと呼ぶ．

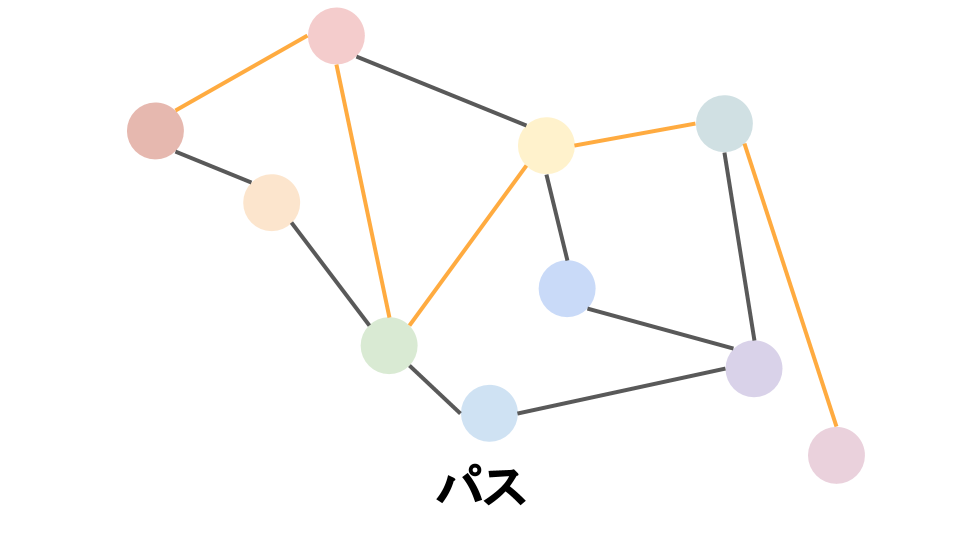
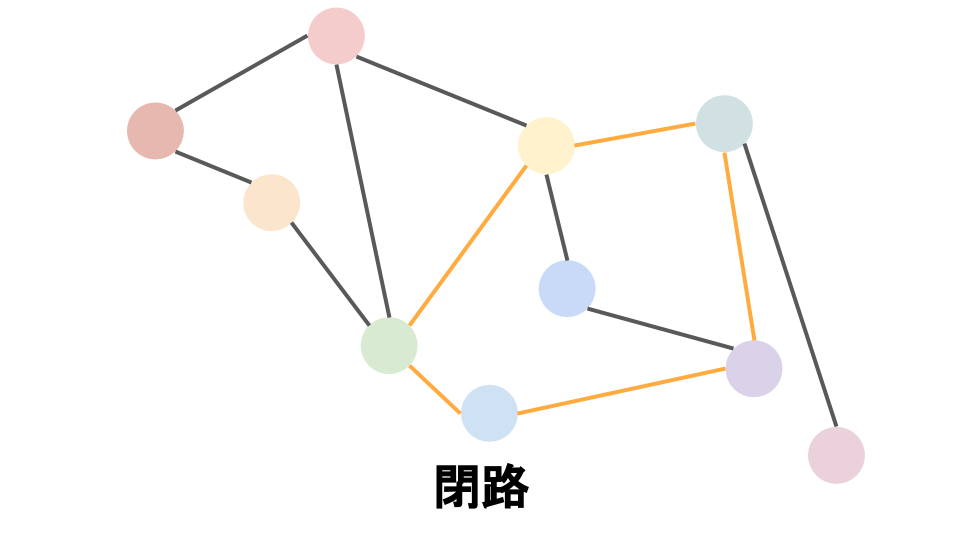
グラフ$G$上の 2 頂点$u$，$v$について，$u$を出発して隣接する頂点をたどることで$v$に到達できるとき，その経路を**$u$-$v$路という．またこのとき$u$をその路の始点**，$v$を終点という．さらに，路のうち，同じ頂点を 2 度以上通らないものをパスという．また，路のうち，始点と終点が等しいものを閉路（またはサイクル）と呼ぶ．

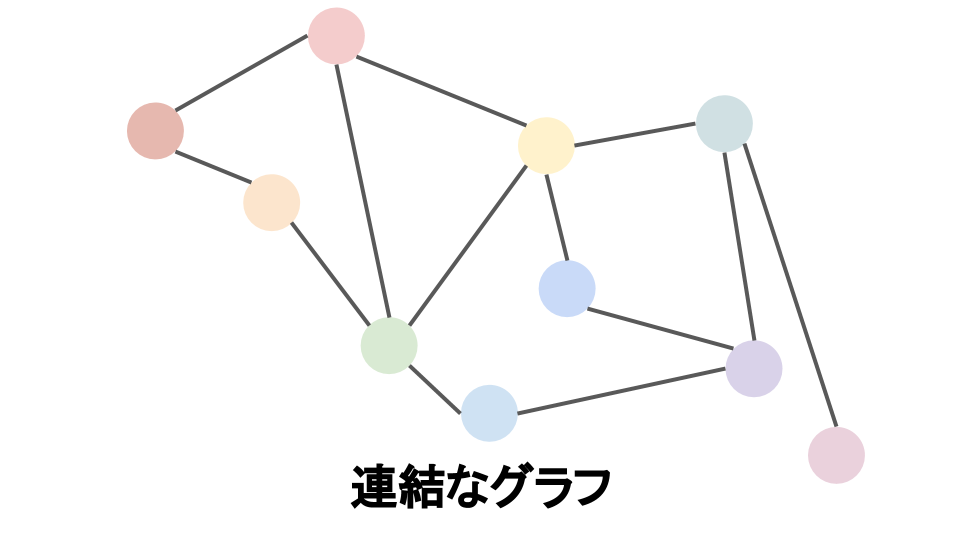
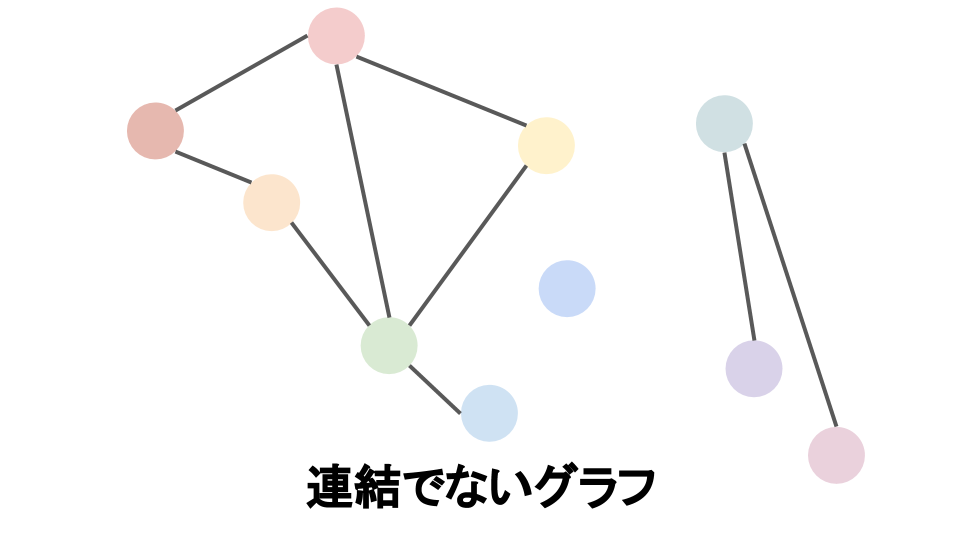
グラフ$G$の任意の 2 頂点$u$，$v$ $\in V$に対して，$u$-$v$パス・$v$-$u$パスが存在するとき，$G$は連結であるという．特に，有向グラフ$G$の任意の 2 頂点$u$，$v$ $\in V$に対して，$u$-$v$パス・$v$-$u$パスが存在するとき，$G$は強連結であるという．

# 計算機上でのグラフの実装

計算機上ではグラフは大きく分けて以下の二通りがある．

隣接リスト

グラフ$G$を構成する各頂点について，その頂点の隣接頂点をリストとして保持することでグラフを表現する．頂点数に対して辺の本数が比較的少ない疎なグラフの実装において（隣接行列表現と比較して）有利なことがある．

隣接行列

グラフ$G$を構成する$n$頂点について，$n \times n$の大きさのテーブルを用意し，頂点$i$-$j$間に辺が生えているとき，そのテーブルの$(i, j)$に1を立てることで辺を表現する．頂点数に対して辺の本数が比較的多い密なグラフの実装において（隣接リスト表現と比較して）有利なことがある．

以下では，グラフを隣接リストとして実装する．

1
2
using Graph = vector<vector<int>>;
Graph G;

例えば，入力が以下のように与えられたとき，グラフ$G$は次のように構築される．

【入力】：
$$ N \space M $$
$$ u_1 \space v_1 $$
$$ u_2 \space v_2 $$
$$ u_3 \space v_3 $$
$$ … $$
$$ u_M \space v_M $$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);
  for (int i = 0; i < M; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
    // G[v].push_back(u);
  }
  return 0;
}

辺に重みのあるグラフであれば，Edgeという辺を表す構造体を定義してやるとわかりやすい．

【入力】：
$$ N \space M $$
$$ u_1 \space v_1 \space w_1 $$
$$ u_2 \space v_2 \space w_2 $$
$$ u_3 \space v_3 \space w_3 $$
$$ … $$
$$ u_M \space v_M \space w_M $$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
#include <bits/stdc++.h>
using namespace std;

struct Edge {
  int to;
  int weight;
  Edge(int to, int weight): to(to), weight(weight) {}
};
using Graph = vector<vector<Edge>>;

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);
  for (int i = 0; i < M; i++) {
    int from, to, weight; cin >> from >> to >> weight;
    G[from].push_back(Edge(to, weight));
    // G[to].push_back(Edge(from, weight));
  }
  return 0;
}

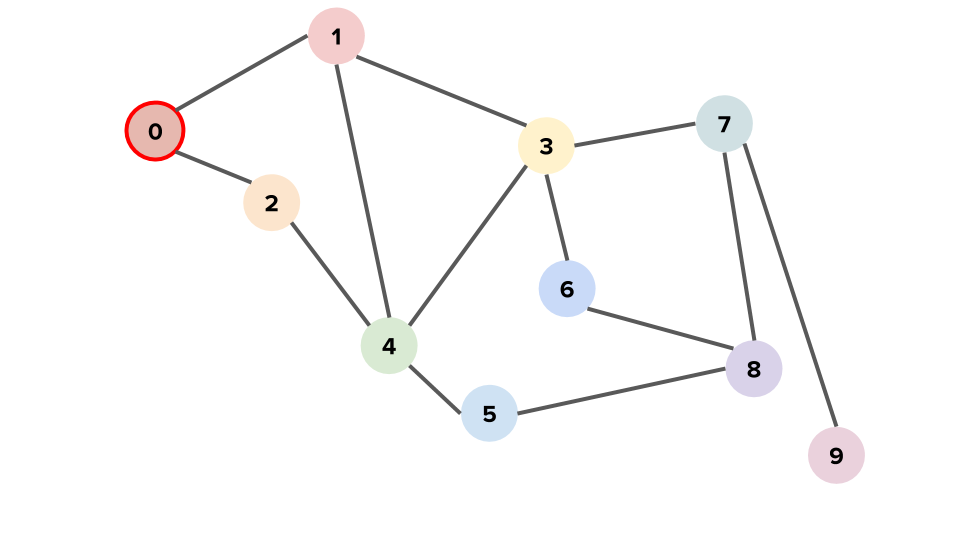
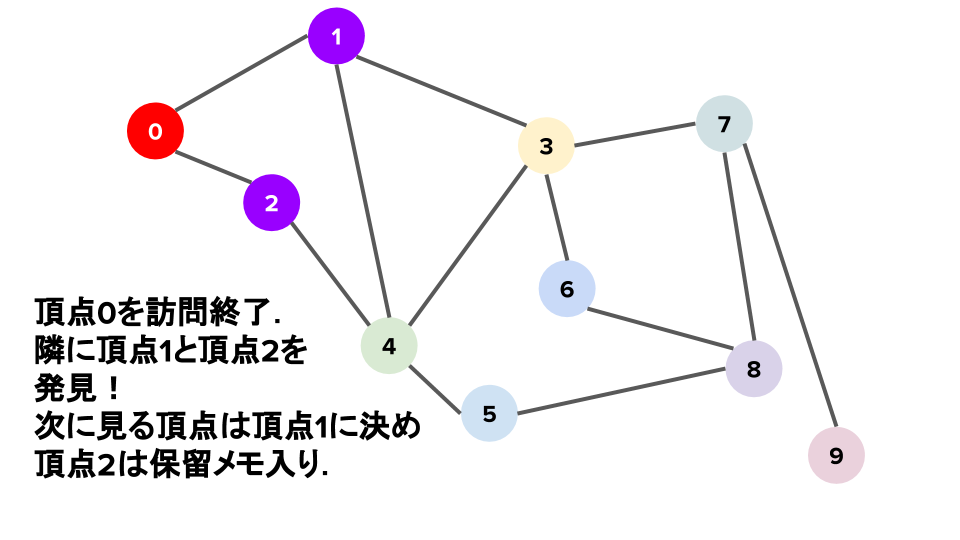
# グラフの探索

一般にグラフ上の探索にはどのような方針が考えられるのだろうか．例えば以下のようなグラフに対する頂点 0 を始点とした探索を考える．

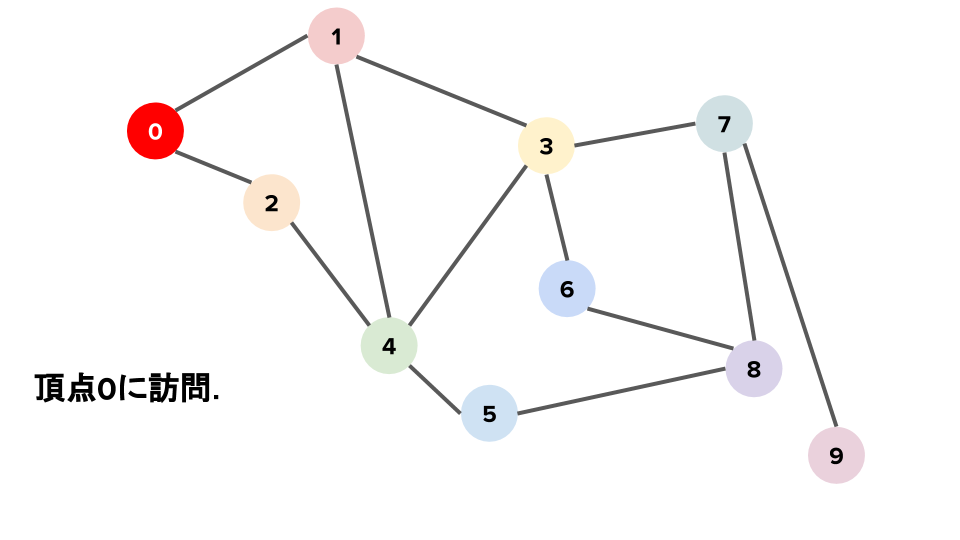
頂点$0$に訪問した後，次に訪問する頂点を探す．つまり頂点$0$の隣接頂点を調べると，頂点$1$と頂点$2$を発見し保留メモに追記する．とりあえず，次に訪問する頂点を頂点$1$に決め，探索を続ける．

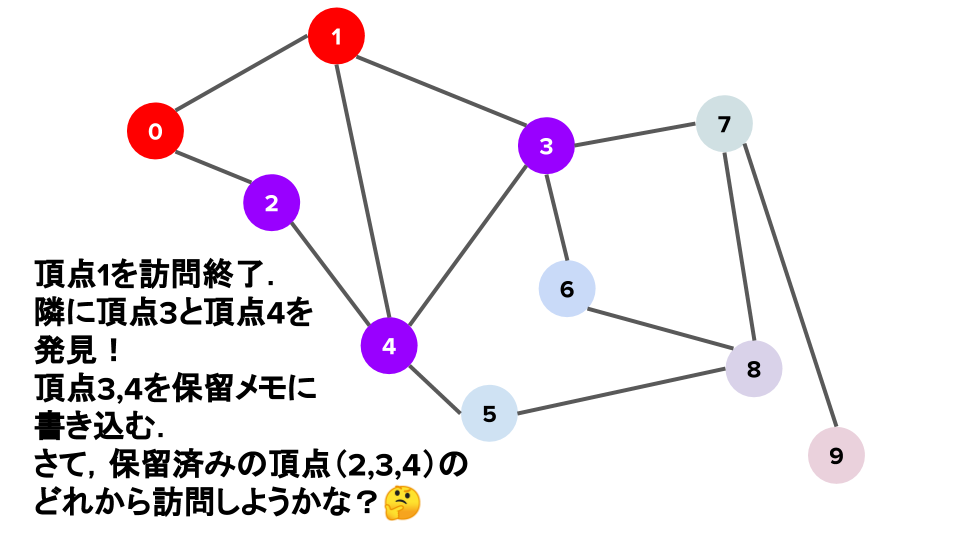
頂点$1$に訪問した後，次に訪問する頂点を探す．つまり，頂点$1$の隣接頂点を調べると，頂点$3$と頂点$4$を発見し保留メモに追記する．．そこで次に訪問する頂点の選び方が 2 通り考えられる．

「後に保留メモに追記した頂点$3$・頂点$4$を，頂点$2$より先に訪問する」
「先に保留メモに追記した頂点$2$を，頂点$3$・頂点$4$より先に訪問する」

「後に保留メモに追記した頂点$3$・頂点$4$を，頂点$2$より先に訪問する」という方針で続く探索を 深さ優先探索 Depth-First Search（DFS） と呼び，「先に保留メモに追記した頂点$2$を，頂点$3$・頂点$4$より先に訪問する」という方針で続く探索を 幅優先探索 Breadth-First Search（BFS） と呼ぶ．

DFS では保留メモの挙動が，Last-In-First-Out なのでスタックや再帰関数で実装することができる．一方で，BFS では保留メモの挙動が，First-In-First-Out なのでキューで実装することができる．

どういう方針で保留メモから次に訪れる頂点を選択するかを一旦脇においておいて，グラフ上の探索を書き下すと

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
has_visited[i]: 頂点iが訪問済みならtrue，そうでないならfalseを格納する配列
suspended: 保留メモ（未訪問かつ存在を発見済みの頂点の集合）

has_visited全体をfalseで初期化・suspendedを空に初期化;
has_visited[始点頂点] = true; suspendedに始点頂点を追加;
while (!suspendedが空) {
  u := suspendedから1つ頂点を取り出す（このときの取り出し方で探索の性格が決まる）;
  for (v: uの隣接頂点) {
    if (has_visited[v]) continue; // すでに訪問済みだったのでスルー
    else {
      has_visited[u] = true; // 訪問したので印をつける
      suspended.append(v);   // 保留メモに追記する
    }
  }
}

また，閉路が存在しないかつ連結であるようなグラフは「木」と呼ばれる．木は，グラフの特殊型であるので，グラフでの探索と同様の議論が木での探索にも言える．

# 深さ優先探索 Depth-Frist Seach（DFS)

グラフ上を探索する手法として有名．「行けるところまで進んで，行き止まりになったら戻って別の道を試す」という方針でグラフ上を探索する．上の説明で言えば「保留メモから LIFO で頂点を取り出す」のが DFS．「保留メモから LIFO で頂点を取り出す」という方針がスタックや再帰関数の性質と一致し実装に用いられる．

# スタックによる DFS の実装

スタックを用いて DFS を実装すると以下のようになる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<bool> has_visited;
stack<int> suspended;
void DFS(const Graph &G, int v) {
  has_visited[v] = true;
  suspended.push(v);

  while (!suspended.empty()) {
    int u = suspended.top(); suspended.pop();
    for (auto w: G[u]) {
      if (has_visited[w]) continue;
      else {
          has_visited[u] = true;
          suspended.push(w);
      }
    }
  }
}

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);
  for (int i = 0; i < M; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
    G[v].push_back(u);
  }

  has_visited.assign(N, false);

  DFS(G, 0);

  return 0;
}

# 再帰関数による DFS の実装

再帰関数を用いて DFS を実装すると以下のようになる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<bool> has_visited;
void DFS(const Graph &G, int v) {
  has_visited[v] = true;

  for (auto u: G[v]) {
    if (has_visited[u]) continue;
    DFS(G, u);
  }
}

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);

  for (int i = 0; i < M; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
    G[v].push_back(u);
  }

  has_visited.assign(N, false);

  DFS(G, 0);
  return 0;
}

# 幅優先探索 Breadth-First Search（BFS）

グラフ上を探索する手法として有名．「分かれ道に遭遇したら，全ての分かれ道についてちょっとずつ等しく訪問していく」という方針でグラフ上を探索する．上の説明で言えば「保留メモから FIFO で頂点を取り出す」のが BFS．「保留メモから FIFO で頂点を取り出す」という方針がキューの性質と一致し実装に用いられる．

# キューによる BFS の実装

キューを用いて BFS を実装すると以下のようになる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<bool> has_visited;
queue<int> suspended;
void BFS(const Graph &G, int v) {
  has_visited[v] = true;
  suspended.push(v);

  while (!suspended.empty()) {
    int u = suspended.front(); suspended.pop();
    for (auto w: G[u]) {
      if (has_visited[w]) continue;
      else {
          has_visited[w] = true;
          suspended.push(w);
      }
    }
  }
}

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);
  for (int i = 0; i < M; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
    G[v].push_back(u);
  }

  has_visited.assign(N, false);

  BFS(G, 0);

  return 0;
}

# BFS にあって DFS にないもの

BFS は全頂点を始点からの辺の本数によってレベル分けすることになる．特に，全ての辺の重さが$1$であるような重み付きグラフで BFS を行うと，その始点からの各頂点の最短距離を求めるアルゴリズムとしても使うことができる．ただし，BFS が最短距離を求めるアルゴリズムとして使えるのは，全ての辺の重さが$1$であるグラフに限ることに注意しなければならない．そうでないグラフなら dijkstra 法など他のアルゴリズムを用いないと正しい答えが得られない．

BFS ですべての辺の重さが$1$であるようなグラフを構成する各頂点の，頂点$0$からの最短距離を求める処理を実装すると次の通り．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<int> distance; // <-- vector<bool> has_visited;
queue<int> suspended;
void BFS(const Graph &G, int v) {
  distance[v] = 0; // 始点の距離は0
  suspended.push(v);

  while (!suspended.empty()) {
    int u = suspended.front(); suspended.pop();
    for (auto w: G[u]) {
      if (distance[w] != -1) continue; // 訪問済みなのでスルー
      else {
          distance[w] = distance[u] + 1; // 頂点wは頂点uの隣接頂点
          suspended.push(w);
      }
    }
  }
}

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);
  for (int i = 0; i < M; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
    G[v].push_back(u);
  }

  for (int i = 0; i < N; i++) distance[i] = -1; // distance[i] == -1 --> 頂点iには未訪問

  BFS(G, 0);

  for (int i = 0; i < N; i++) {
    cout << "node[" << i << "]: " << distance[i] << endl;
  }
  return 0;
}

# グラフ探索の例題

# 到達可能性判定

2 頂点$s$，$t$ $\in V$が与えられ，$s$から$t$へ辺をたどって到達することが可能であるかを判定する問題．単純に，$s$を始点とした DFS または BFS を実行し，has_visited[s]を確かめれば良い．

スタックを使った DFS による解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<bool> has_visited;
stack<int> suspended;
void DFS(const Graph &G, int v) {
  has_visited[v] = true;
  suspended.push(v);

  while (!suspended.empty()) {
    int u = suspended.top(); suspended.pop();
    for (auto w: G[u]) {
      if (has_visited[w]) continue;
      else {
          has_visited[u] = true;
          suspended.push(w);
      }
    }
  }
}

int main() {
  int N, M, s, t; cin >> N >> M >> s >> t;
  Graph G(N);
  for (int i = 0; i < M; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
  }
  has_visited.assign(N, false);
  DFS(G, s);
  if (has_visited[t]) cout << "Yes" << endl;
  else cout << "No" << endl;
  return 0;
}

再帰を使った DFS による解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<bool> has_visited;
void DFS(const Graph &G, int v) {
  has_visited[v] = true;

  for (auto w: G[v]) {
    if (has_visited[w]) continue;
    DFS(G, w);
  }
}

int main() {
  int N, M, s, t; cin >> N >> M >> s >> t;
  Graph G(N);
  for (int i = 0; i < M; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
  }
  has_visited.assign(N, false);
  DFS(G, s);
  if (has_visited[t]) cout << "Yes" << endl;
  else cout << "No" << endl;
  return 0;
}

BFS による解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<bool> has_visited;
queue<int> suspended;
void BFS(const Graph &G, int v) {
  has_visited[v] = true;
  suspended.push(v);

  while (!suspended.empty()) {
    int u = suspended.front(); suspended.pop();
    for (auto w: G[u]) {
      if (has_visited[w]) continue;
      else {
          has_visited[u] = true;
          suspended.push(w);
      }
    }
  }
}

int main() {
  int N, M, s, t; cin >> N >> M >> s >> t;
  Graph G(N);
  for (int i = 0; i < M; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
  }
  has_visited.assign(N, false);
  BFS(G, s);
  if (has_visited[t]) cout << "Yes" << endl;
  else cout << "No" << endl;
  return 0;
}

# グリッドグラフ

グラフが二次元グリッドとして与えられるような問題も頻出である．グリッド形式でのグラフの入力はたいてい以下のような形式である．

【入力】

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
10 10       // 盤面サイズ（縦・横）
s.........  // s: スタート位置
#########.  // g: ゴール位置
#.......#.  // 「.」は通路
#..####.#.  // 「#」は壁（進むことができない）
##....#.#.
#####.#.#.
g.#.#.#.#.
#.#.#.#.#.
#.#.#.#.#.
#.....#...

与えられた迷路内を，上下左右に移動しながら通路マス.のみを通ってsからgまでたどり着けるかを判定する．

スタックを使った DFS による解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>
using namespace std;

const int dx[4] = {1, 0, -1, 0};
const int dy[4] = {0, 1, 0, -1};

int H, W;
vector<string> maze;

bool has_visited[510][510];
stack<pair<int, int>> suspended;
void DFS(int h, int w) {
  suspended.push(make_pair(h, w));
  has_visited[h][w] = true;

  while (!suspended.empty()) {
    int ch, cw;
    tie(ch, cw) = suspended.top(); suspended.pop();
    for (int dir = 0; dir < 4; dir++) {
      int nh = ch + dx[dir];
      int nw = cw + dy[dir];
      if (nh < 0 || H <= nh || nw < 0 || W <= nw) continue; // 場外なので進めず
      if (maze[nh][nw] == '#') continue; // 壁なので進めず
      if (has_visited[nh][nw]) continue;
      else {
        has_visited[ch][cw] = true;
        suspended.push(make_pair(nh, nw));
      }
    }
  }
}

int main(){
  cin >> H >> W;
  maze.resize(H);
  for (int h = 0; h < H; h++) cin >> maze[h];

  int sh, sw, gh, gw;
  for (int h = 0; h < H; h++) {
    for (int w = 0; w < W; w++) {
      if (maze[h][w] == 's') sh = h, sw = w;
      if (maze[h][w] == 'g') gh = h, gw = w;
    }
  }

  memset(has_visited, 0, sizeof(has_visited));

  DFS(sh, sw);

  if (has_visited[gh][gw]) cout << "Yes" << endl;
  else cout << "No" << endl;
  return 0;
}

再帰を使った DFS による解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <bits/stdc++.h>
using namespace std;

const int dx[4] = {1, 0, -1, 0};
const int dy[4] = {0, 1, 0, -1};

int H, W;
vector<string> maze;

bool has_visited[510][510];
void DFS(int h, int w) {
  has_visited[h][w] = true;

  for (int dir = 0; dir < 4; dir++) {
    int nh = h + dx[dir];
    int nw = w + dy[dir];

    if (nh < 0 || H <= nh || nw < 0 || W <= nw) continue; // 場外なので進めず
    if (maze[nh][nw] == '#') continue; // 壁なので進めず

    if (has_visited[nh][nw]) continue;

    DFS(nh, nw);
  }
}

int main(){
  cin >> H >> W;
  maze.resize(H);
  for (int h = 0; h < H; h++) cin >> maze[h];

  int sh, sw, gh, gw;
  for (int h = 0; h < H; h++) {
    for (int w = 0; w < W; w++) {
      if (maze[h][w] == 's') sh = h, sw = w;
      if (maze[h][w] == 'g') gh = h, gw = w;
    }
  }

  memset(has_visited, 0, sizeof(has_visited));

  DFS(sh, sw);

  if (has_visited[gh][gw]) cout << "Yes" << endl;
  else cout << "No" << endl;
  return 0;
}

BFS による解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>
using namespace std;

const int dx[4] = {1, 0, -1, 0};
const int dy[4] = {0, 1, 0, -1};

int H, W;
vector<string> maze;

bool has_visited[510][510];
queue<pair<int, int>> suspended;
void BFS(int h, int w) {
  suspended.push(make_pair(h, w));
  has_visited[h][w] = true;

  while (!suspended.empty()) {
    int ch, cw;
    tie(ch, cw) = suspended.front(); suspended.pop();
    for (int dir = 0; dir < 4; dir++) {
      int nh = ch + dx[dir];
      int nw = cw + dy[dir];
      if (nh < 0 || H <= nh || nw < 0 || W <= nw) continue; // 場外なので進めず
      if (maze[nh][nw] == '#') continue; // 壁なので進めず
      if (has_visited[nh][nw]) continue;
      else {
        has_visited[ch][cw] = true;
        suspended.push(make_pair(nh, nw));
      }
    }
  }
}

int main(){
  cin >> H >> W;
  maze.resize(H);
  for (int h = 0; h < H; h++) cin >> maze[h];

  int sh, sw, gh, gw;
  for (int h = 0; h < H; h++) {
    for (int w = 0; w < W; w++) {
      if (maze[h][w] == 's') sh = h, sw = w;
      if (maze[h][w] == 'g') gh = h, gw = w;
    }
  }

  memset(has_visited, 0, sizeof(has_visited));

  BFS(sh, sw);

  if (has_visited[gh][gw]) cout << "Yes" << endl;
  else cout << "No" << endl;
  return 0;
}

# 連結成分のカウント

連結とは限らない（つまりぶった切れているかもしれない）グラフが与えられ，その連結成分の個数を数える．これも単純にまだ探索していない頂点を 1 つ選んで$v$とし，$v$を始点とする DFS または BFS を実行することを，全頂点が探索済みになるまで繰り返せば良い．

スタックを使った DFS による解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<bool> has_visited;
stack<int> suspended;
void DFS(const Graph &G, int v) {
  has_visited[v] = true;
  suspended.push(v);
  while (!suspended.empty()) {
    int u = suspended.top(); suspended.pop();
    for (auto w: G[u]) {
      if (has_visited[w]) continue;
      else {
        has_visited[u] = true;
        suspended.push(w);
      }
    }
  }
}

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);
  for (int i = 0; i < M; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
    G[v].push_back(u);
  }

  int cnt = 0;
  has_visited.assign(N, false);
  for (int v = 0; v < N; v++) {
    if (has_visited[v]) continue;
    DFS(G, v);
    cnt++;
  }
  cout << cnt << endl;
  return 0;
}

再帰を使った DFS による解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<bool> has_visited;
void DFS(const Graph &G, int v) {
  has_visited[v] = true;
  for (auto w: G[v]) {
    if (has_visited[w]) continue;
    else DFS(G, w);
  }
}

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);
  for (int i = 0; i < M; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
    G[v].push_back(u);
  }

  int cnt = 0;
  has_visited.assign(N, false);
  for (int v = 0; v < N; v++) {
    if (has_visited[v]) continue;
    DFS(G, v);
    cnt++;
  }
  cout << cnt << endl;
  return 0;
}

BFS による解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<bool> has_visited;
queue<int> suspended;
void BFS(const Graph &G, int v) {
  has_visited[v] = true;
  suspended.push(v);
  while (!suspended.empty()) {
    int u = suspended.front(); suspended.pop();
    for (auto w: G[u]) {
      if (has_visited[w]) continue;
      else {
        has_visited[u] = true;
        suspended.push(w);
      }
    }
  }
}

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);
  for (int i = 0; i < M; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
    G[v].push_back(u);
  }

  int cnt = 0;
  has_visited.assign(N, false);
  for (int v = 0; v < N; v++) {
    if (has_visited[v]) continue;
    BFS(G, v);
    cnt++;
  }
  cout << cnt << endl;
  return 0;
}

# 二部グラフ判定

与えられたグラフが二部グラフであるかを判定する．二部グラフとは「全頂点を白または黒に塗っていくとき，白頂点同士が辺で結ばれることがなくかつ黒頂点同士が辺で結ばれることがないように頂点を塗り分けられるグラフ」のことである．

判定方法は簡単である．適当な頂点を白もしくは黒に塗ったとき，その頂点を始点に自動的に隣接頂点たちの色が次々に決まる．塗りながら，隣接する頂点が同じ色になってしまうかを確認すれば判定できる．全頂点を塗ることができれば，そのグラフは二部グラフであると言える．

また，配列has_visitedは未訪問であることを表す色を導入することで，頂点の色を保持する配列にまとめさせることができる．

再帰を使った DFS による解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;
vector<int> color; // color[i]: 0 = 黒, 1 = 白, -1 = 未訪問
bool DFS(const Graph &G, int v, int current_color = 0) {
  color[v] = current_color;
  for (auto w: G[v]) {
    if (color[w] != -1) {
      if (color[w] == current_color) return false;
      continue;
    }
    if (!DFS(G, w, 1 - current_color)) return false;
  }
  return true;
}

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);
  for (int i = 0; i < M; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
    G[v].push_back(u);
  }
  color.assign(N, -1);
  bool is_bipartite = true;
  for (int v = 0; v < N; v++) {
    if (color[v] != -1) continue;
    if (!DFS(G, v)) is_bipartite = false;
  }

  if (is_bipartite) cout << "Yes" << endl;
  else cout << "No" << endl;
  return 0;
}

BFS では「始点頂点からの距離によって頂点をレベル分けする」ことになり，与えられたグラフが二部グラフなら始点からの距離が偶数なら始点と同じ色，奇数なら異なる色となる．ここで，互いに隣接する頂点間では始点からの距離が 1 だけことなるので，「グラフが二部グラフである」と「BFS によって計算される各頂点の始点からの距離が等しい 2 頂点は隣接しない」は同値となる．

BFS による解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);
  for (int i =0 ; i < M; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
    G[v].push_back(u);
  }

  bool is_bipartite = true;
  vector<int> distance(N, -1);
  queue<int> suspended;
  for (int v = 0; v < N; v++) {
    if (distance[v] != -1) continue;
    distance[v] = 0;
    suspended.push(v);
    while (!suspended.epmty()) {
      int v = suspended.front(); suspended.pop();
      for (auto w: G[v]) {
        if (dist[w] == -1) {
          dist[w] = dist[v] + 1;
          suspended.push(w);
        } else {
          if (dist[v] == dist[w]) is_bipartite = false;
        }
      }
    }
  }

  if (is_bipartite) cout << "Yes" << endl;
  else cout << "No" MM endl;
  return 0;
}

# 木に対する DFS

「木」は「閉路のない連結なグラフ」である．木に対する DFS では，次に訪問する頂点を探すときに，必ず「親がすでに訪問済みである」とマークされている．このことを利用することで，根のない木に対して，与えられた頂点を根としたときの根付き木を計算することができる．以下では，与えられたグラフ$G$を，頂点$0$を根とした根付き木と見たときの，各頂点の深さ（根からの距離）とその頂点を根とする部分木のサイズを計算する．頂点の深さは，根からの距離であり，行きがけ時に決まる．なぜなら，ある頂点の深さは，その頂点の親の深さに 1 を足したものである．一方で，部分木のサイズは，帰りがけ時に決まる．なぜなら，自身を根とする部分木のサイズは，自分の子供を根とする部分木のサイズの総和に 1 足したものである．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<int> depth;
vector<int> subtree_size;

void DFS(const Graph &G, int v, int p, int d) {
  // 行きがけ時
  depth[v] = d;

  for (auto w: G[v]) {
    if (w == p) continue;
    DFS(G, w, v);
  }

  // 帰りがけ時
  subtree_size[v] = 0;
  for (auto child: G[v]) {
    if (child == p) continue; // 隣接頂点が親しかいない．つまり木から見ると葉
    subtree_size[v] += subtree_size[c];
  }
  subtree_size[v] += 1; // 自分自身
}

int main() {
  int N; cin >> N; // 木の辺数 = 頂点数 - 1
  Graph G(N);
  for (int i = 0; i < N-1; i++) {
    int u, v; cin >> u >> v;
    G[u].push_back(v);
    G[v].push_back(u);
  }
  int root = 0;
  depth.assign(N, 0);
  subtree_size.assign(N, 0);
  DFS(G, root, -1); // グラフGを，頂点0を根とした根付き木としてDFS

  for (int v = 0; v <  N; v++) {
    cout << "node[" << v  "]: depth = " << depth[v] << ", subtree_size = " << subtree_size[v] << endl;
  }
  return 0;
}

一般に，子ノードの情報を用いて親ノードの情報を更新する処理を木 DPという．行きがけ時には「親ノードの情報を子ノードに配る」ような処理をし，帰りがけ時には「子ノードの情報を親ノードに集めて親ノードの情報を更新する」ような処理をすると良い．

# トポロジカルソート

トポロジカルソートとは，閉路の存在しない有向グラフ（このようなグラフを DAG という）に対して，辺の向きが揃うように頂点を並べるようなソートのことを指し，ソフトウェアのモジュール間・ソースコード間の依存関係を解決するような場面で用いられる．また，DAG であることはトポロジカルソートが可能であることと同値であるらしい．

トポロジカルソートでは，その頂点を始点とする辺が 0 本であるような頂点（シンクノード）が末尾に来る.シンクノードを取り除き，その頂点に向かっていた辺を削除すると，新たにシンクノードになる頂点が発生する．新たに発生したシンクノードから適当に一つ選び削除し同様のことを行う．これをすべての頂点が削除されるまで行い，頂点の削除された逆順を出力するとトポロジカルソートが実現できる．この方法だと逆向きの BFS っぽい挙動となる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);

  vector<int> out_degree(N); // out_degree[i]: 頂点iを始点とする辺の本数
  for (int i = 0; i < M; i++) {
    int from, to; cin >> from >> to;
    G[to].push_back(from); // 辺を逆向きに保存する
    out_degree[from]++;
  }

  queue<int> q;
  for (int i = 0;i < N; i++) if (out_degree == 0) q.push(i); // シンクノードをキューに突っ込む

  vector<int> order; // order[i]: 頂点iのトポロジカルソートにおける順位の逆順
  while (!q.empty()) {
    int v = q.front(); q.pop();
    order.push_back(v);
    for (auto neighbor: G[v]) {
      out_degree[neighbor]--; // シンクノードに向かって生えていた辺を消す
      if (out_degree[neighbor] == 0) q.push(neighbor);
    }
  }
  reverse(order.begin(), order.end());
  for (auto v: order) cout << v << endl;
  return 0;
}

ここで，DFS の帰りがけ順を考えると，これはまさしくトポロジカルソートとなる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

void DFS(const Graph &G, int v, vector<bool> &has_visited, vector<int> &order) {
  has_visited[v] = true;
  for (auto w: G[v]) {
    if (has_visited[w]) continue;
    DFS(G, w, has_visited, order);
  }

  // 帰りがけ時
  order.push_back(v);
}

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);

  for (int i = 0; i < M; i++) {
    int from, to; cin >> from >> to;
    G[from].push_back(to);
  }

  vector<bool> has_visited(N, false);
  vector<int> order;

  for (int v = 0; v < N; v++) {
    if (has_visited[v]) continue;
    DFS(G, v, has_visited, order);
  }

  reverse(order.begin(), order.end());
  for (auto v: order) cout << v << endl;
  return 0;
}

# 閉路検出

グラフに閉路が存在するかを検出する問題．BFS っぽいトポロジカルソートの手法を考慮すると，サイクルに含まれる頂点はシンクノードになることがないので，トポロジカルソートできる範囲でトポロジカルソートした後に，キューに入ったことがない頂点が存在すれば，閉路が存在することがわかる．

以下は，サイクルを 1 つ含むことが保証された無向グラフに対して，2 頂点$a$，$b$がともにそのサイクル上にあるときは2を，そうでないときは1を出力せよという問題の解答である．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

int main() {
  int N; cin >> N; // サイクルを1つ含むグラフなので辺数もN
  Graph G(N);
  vector<int> degree(N, 0);
  for (int i = 0; i < N; i++) {
    int u, v; cin >> u >> v;
    u--; v--;
    G[u].push_back(v);
    G[v].push_back(u);
    degree[u]++; degree[v]++;
  }

  queue<int> q;
  for (int i = 0; i < N; i++) if (degree[i] == 1) q.push(i);

  vector<bool> has_enqueued(N, false); // has_enqueued[i]: 頂点iがキューに入ったことがあるか
  while (!q.empty()) {
    int v = q.front(); q.pop();
    has_enqueued[v] = true;
    for (auto w: G[v]) {
      degree[w]--;
      if (degree[w] == 1) q.push(w);
    }
  }

  int Q; cin >> Q;
  for (int _ = 0; _ < Q; _++) {
    int a, b; cin >> a >> b; a--; b--;
    if (!has_enqueued[a] && !has_enqueued[b]) cout << 2 << endl;
    else cout << 1 << endl;
  }
}

また，与えられたグラフに閉路があるとき，ある頂点$v$に対して，$v$から到達することができる全頂点の探索の終了より前に（つまり帰りがけ時になる前に）$v$に戻って来ることができることと同値である．これを検知してやっても閉路検知になる．これを実現するためには，has_visited[i]: 頂点iを行きがけ順の意味で訪問済み，has_finished[i]: 頂点iを帰りがけ順の意味で訪問終了とする配列を用意れば良い．また，閉路を復元までしたい場合には，行きがけ時に積み，帰りがけ時に取り出すスタックを用意すると，閉路を検知した時点でのスタックの中身が閉路を構成する頂点になっている．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<bool> has_visited, has_finished;
int pos = -1;
stack<int> history;

void DFS(const Graph &G, int v, int p) {
  has_visited[v] = true; // 行きがけ順の意味で訪問済み
  history.push(v);
  for (auto w: G[v]) {
    if (w == p) continue;
    if (has_finished[w]) continue;
    if (has_visited[w] && !has_finished[w]) { // 行きがけ順の意味で訪問済みなのに帰りがけ順の意味で未訪問
      pos = w;
      return;
    }
    DFS(G, w, v);
    if (pos != -1) return;
  }
  history.pop();
  has_finished[v] = true; // 帰りがけ順の意味で訪問済み
}

int main() {
  int N; cin >> N;
  Graph G(N);
  for (int i = 0; i < N; i++) {
    int u, v; cin >> u >> v; u--; v--;
    G[u].push_back(v);
    G[v].push_back(u);
  }
  has_visited.assign(N, false);
  has_finished.assign(N, false);
  pos = -1;
  DFS(G, 0, -1);

  set<int> cycle;
  while (!history.empty()) {
    int v = history.pop();
    cycle.insert(v);
    history.pop();
    if (v == pos) break;
  }

  int Q; cin >> Q;
  for (int _ = 0; _ < Q; _++) {
    int a, b; cin >> a >> b; a--; b--;
    if (cycle.count(a) && cycle.count(b)) cout << 2 << endl;
    else cout << 1 << endl;
  }
  return 0;
}

# グラフ探索の練習問題

# 解説

# ALDS 1-11 B

基本問題．再帰の DFS が書きやすい．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<bool> has_visited;
vector<int> d; // 行きがけのタイムスタンプ
vector<int> f; // 帰りがけのタイムスタンプ
int tick = 0;
void DFS(const Graph &G, int v) {
  has_visited[v] = true;
  tick++;
  d[v] = tick;
  for (auto w: G[v]) {
    if (has_visited[w]) continue;
    DFS(G, w);
  }
  tick++;
  f[v] = tick;
}

int main() {
  int N; cin >> N;
  Graph G(N);
  has_visited.resize(N); has_visited.assign(N, false);
  d.resize(N); d.assign(N, 0);
  f.resize(N); f.assign(N, 0);
  for (int i = 0; i < N; i++) {
    int u, k;
    cin >> u >> k; u--;
    G[u].resize(0);
    int v;
    for (int i = 0; i < k; i++) {
      cin >> v; v--;
      G[u].push_back(v);
    }
  }
  for (int i = 0; i < N; i++) {
    if (!has_visited[i]) DFS(G, i);
  }
  for (int i = 0; i < N; i++) {
    cout << i+1 << " " << d[i] << " " << f[i] << endl;
  }
  return 0;
}

# AOJ 1160

グリッドグラフの連結成分をカウントする問題．深さ優先探索でカウントしていく．陸が1で海が0であるが，訪問済みのマス目を0で潰していくことで配列has_visitedを用意せずとも実装できる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h>
using namespace std;

int H, W;
vector<vector<int>> field;

void DFS(int h, int w) {
  field[h][w] = 0; // 訪問した陸のマスを海にしてしまう

  for (int dh = -1; dh <= 1; dh++) {
    for (int dw = -1; dw <= 1; dw++) {
      int nh = h + dh;
      int nw = w + dw;
      if (nh < 0 || H <= nh || nw < 0 || W <= nw) continue;
      if (field[nh][nw] == 0) continue;

      DFS(nh, nw);
    }
  }
}

int main() {
  while (cin >> W >> H) {
    if (H == 0 || W == 0) break;
    field.assign(H, vector<int>(W, 0));
    for (int h = 0; h < H; h++) {
      for (int w = 0; w < W; w++) {
        cin >> field[h][w];
      }
    }

    int cnt = 0;
    for (int h = 0; h < H; h++) {
      for (int w = 0; w < W; w++) {
        if (field[h][w] == 0) continue;
        DFS(h, w);
        cnt++;
      }
    }
    cout << cnt << endl;
  }
  return 0;
}

# ABC 138 D

親ノードの情報を子ノードに配るので，DFS で行きがけにカウンタの値を更新する．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<long long> counters;
vector<bool> has_visited;
void DFS(const Graph &G, int v) {
  has_visited[v] = true;
  for (auto w: G[v]) {
    if (has_visited[w]) continue;
    else {
      counters[w] += counters[v];
      DFS(G, w);
    }
  }
}

int main() {
  int N, Q; cin >> N >> Q;
  Graph G(N);
  has_visited.resize(N);
  has_visited.assign(N, false);
  counters.resize(N);
  counters.assign(N, 0);
  for (int i = 0; i < N-1; i++) {
    int a, b; cin >> a >> b; a--; b--;
    G[a].push_back(b);
    G[b].push_back(a);
  }
  for (int i = 0; i < Q; i++) {
    int p; cin >> p; p--;
    long long x; cin >> x;
    counters[p] += x;
  }
  DFS(G, 0);
  for (int i = 0; i < N; i++) {
    if (i != N-1) cout << counters[i] << " ";
    else cout << counters[i] << endl;
  }
  return 0;
}

# JOI2009 予選 4

薄氷の地図をグリッドグラフとみなすと，割ることのできる薄氷の枚数はグラフの深さに対応する．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;
const int dx[4] = {1, 0, -1, 0};
const int dy[4] = {0, -1, 0, 1};

int H, W, ans = -1;

vector<vector<bool>> has_broken;
void DFS(const Graph &G, int h, int w, int d) {
  ans = max(ans, d);
  has_broken[h][w] = true;
  for (int dir = 0; dir < 4; dir++) {
    int nh = h + dx[dir];
    int nw = w + dy[dir];
    if (nh < 0 || H <= nh || nw < 0 || W <= nw) continue;
    if (has_broken[nh][nw]) continue;
    if (!G[nh][nw]) continue;
    DFS(G, nh, nw, d+1);
  }
  has_broken[h][w] = false;
}

int main() {
  cin >> W;
  cin >> H;

  has_broken.resize(H);
  for (int i = 0; i < H; i++) has_broken[i].resize(W);
  Graph G(H);
  for (int i = 0; i < H; i++) {
    G[i].resize(W);
  }
  for (int i = 0; i < H; i++) {
    for (int j = 0; j < W; j++) {
      int x; cin >> x;
      G[i][j] = x;
    }
  }
  for (int h = 0; h < H; h++) {
    for (int w = 0; w < W; w++) {
      if (!G[h][w]) continue;
      DFS(G, h, w, 1);
    }
  }
  cout << ans << endl;
  return 0;
}

# ARC 31 B

グリッドグラフの連結成分カウント問題．DFS で解ける．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<string>;

const int dh[4] = {1, 0, -1, 0};
const int dw[4] = {0, 1, 0, -1};
const int H = 10, W = 10;

void DFS(Graph &G, int h, int w) {
  G[h][w] = '*'; // 訪問済み
  for (int dir = 0; dir < 4; dir++) {
    int nh = h + dh[dir];
    int nw = w + dw[dir];
    if (nh < 0 || H <= nh || nw < 0 || W <= nw) continue;
    if (G[nh][nw] == '*') continue;
    if (G[nh][nw] == 'x') continue;
    else {
      DFS(G, nh, nw);
    }
  }
}

int check(Graph &G) {
  int cnt = 0;
  for (int h = 0; h < H; h++) {
    for (int w = 0; w < W; w++) {
      if (G[h][w] == 'o') {
        DFS(G, h, w);
        cnt++;
      }
    }
  }
  return cnt;
}

int main() {
  Graph G(H);
  for (int h = 0; h < H; h++) cin >> G[h];
  for (int h = 0; h < H; h++) {
    for (int w = 0; w < W; w++) {
      if (G[h][w] == 'x') {
        G[h][w] = 'o';
        if (check(G) == 1) {
          cout << "YES" << endl;
          return 0;
        }
        for (int h = 0; h < H; h++) for (int w = 0; w < W; w++) if (G[h][w] == '*') G[h][w] = 'o';
        G[h][w] = 'x';
      }
    }
  }
  cout << "NO" << endl;
  return 0;
}

# ABC 126 D

二部グラフ判定問題に似ている．「同じ色に塗られた任意の 2 頂点についてその距離が偶数」という条件から，ある 1 つ頂点の色を決めてしまえば，他の頂点の色は自動的に決定してしまう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
using namespace std;

struct Edge {
  int to;
  int weight;
  Edge(int to, int weight): to(to), weight(weight) {}
};

using Tree = vector<vector<Edge>>;

// 1: 黒, 0: 白, -1:未訪問
vector<int> color;

bool DFS(const Tree &T, int v, int current_color = 0) {
  color[v] = current_color;
  for (auto e: T[v]) {
    if (color[e.to] != -1) {
      if ((e.weight%2 == 1 && color[e.to] == current_color) &&
          (e.weight%2 == 0 && color[e.to] != current_color)) {
            return false;
      } else {
        continue;
      }
    }

    if (e.weight%2 == 0) {
      if (!DFS(T, e.to, current_color)) {
        return false;
      }
    } else {
      if (!DFS(T, e.to, 1 - current_color)) {
        return false;
      }
    }
  }
  return true;
}

int main(){
  int N; cin >> N;
  Tree T(N);
  for (int i = 0; i < N-1; i++) {
    int u, v, w; cin >> u >> v >> w; u--; v--;
    T[u].push_back(Edge(v, w));
    T[v].push_back(Edge(u, w));
  }
  color.assign(N, -1);
  for (int v = 0; v < N; v++) {
    if (color[v] != -1) continue;
    if (DFS(T, v)) break;
  }
  for (int v = 0; v < N; v++) cout << color[v] << endl;
  return 0;
}

# CODE FSTIVAL2017 qualB C

🍎さんが持っているのは，$N$頂点の連結な無向グラフ．操作によって頂点$u$-頂点$v$には長さ$3$のパスと長さ$1$のパスが存在することになる．奇数長のパスを持つ 2 頂点$u$，$v$ $\in V$に対して，「操作」を繰り返すことで$u$，$v$を直接結ぶ辺が登場する．これは帰納的に証明できる．「グラフに奇数長のパスが存在するかどうか」はそのグラフが二部グラフであるかどうかによって変わる．

まず，グラフ$G$が二部グラフであるときを考える．$G$は二部グラフなので頂点を黒・白で塗り分けることができる．異なる色で塗られた任意の頂点対を取ると，$G$は連結なグラフなので，その頂点対間にはパスが存在して，その長さは奇数である．ゆえに，「操作」を繰り返すことでいつかはその頂点対間には辺が張られる．よって，$G$が二部グラフであるとき，「操作」を繰り返すことで任意の黒色頂点-任意の白色頂点間に辺を張ることができる．追加できる辺の本数は，黒色頂点数と白色頂点数の積からすでに存在する辺数$M$を引いた値となる．

次にグラフ$G$が二部グラフでないときを考える．$G$が二部グラフでないならば，同じ色で塗られた頂点を結ぶ辺が存在することになる．$G$は連結でもあるので$V$内の任意の 2 頂点間にはパスが存在する．よって，同じ色で塗られた頂点を結ぶ辺の端点を含む長さが奇数の閉路が$G$に存在することになる．この閉路を用いることで，$G$内の任意の 2 頂点間に長さが奇数のパスを見つけることができる．$G$は連結なので，$V$内の任意の 2 頂点間にはパスが存在し，たとえそれが偶数であっても，奇数長の閉路を余分に経ることでそのパスの長さを奇数にすることができる．奇数長のパスが存在するときその端点の頂点は「操作」を繰り返すことで直接結ぶ辺が張られるので，$G$は完全グラフになっていく．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<int> color;
bool DFS(const Graph &G, int v, int current_color = 0) {
  color[v] = current_color;
  for (auto w: G[v]) {
    if (color[w] != -1) {
      if (color[w] == current_color) return false;
      else continue;
    }
    if (!DFS(G, w, 1 - current_color)) return false;
  }
  return true;
}

int main() {
  int N, M; cin >> N >> M;
  Graph G(N);
  for (int i = 0; i < M; i++) {
    int a, b; cin >> a >> b; a--; b--;
    G[a].push_back(b);
    G[b].push_back(a);
  }
  color.assign(N, -1);
  bool is_bipartite = true;
  for (int v = 0; v < N; v++) {
    if (color[v] != -1) continue;
    if (!DFS(G, v)) is_bipartite = false;
  }
  if (is_bipartite) {
    int B = 0, W = 0;
    for (int v = 0; v < N; v++) {
      if (color[v] == 0) W++;
      else if (color[v] == 1) B++;
    }
    cout << W*B - M << endl;
  } else {
    cout << N*(N-1)/2 - M << endl;
  }
  return 0;
}

# ALDS 1-11 C

幅優先探索の基本問題．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>
using namespace std;

using Graph = vector<vector<int>>;

vector<int> dist;
void BFS(const Graph &G, int v) {
  queue<int> q;
  dist[v] = 0;
  q.push(v);

  while (!q.empty()) {
    int w = q.front(); q.pop();
    for (auto nn: G[w]) {
      if (dist[nn] != -1) continue;
      dist[nn] = dist[w] + 1;
      q.push(nn);
    }
  }
}

int main() {
  int N; cin >> N;
  Graph G(N);
  for (int i = 0; i < N; i++) {
    int u, k; cin >> u >> k; u--;
    for (int j = 0; j < k; j++) {
      int v; cin >> v; v--;
      G[u].push_back(v);
    }
  }
  dist.assign(N, -1);

  BFS(G, 0);

  for (int i = 0; i < N; i++) {
    cout << i+1 << " " << dist[i] << endl;
  }
  return 0;
}

# ABC 7 C

グリッド形式での迷路探索．「最小手数」がほしいので BFS が手軽．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>
using namespace std;

const int dh[4] = {1, 0, -1, 0};
const int dw[4] = {0, 1, 0, -1};

using Graph = vector<string>;
queue<pair<int, int>> suspended;
vector<vector<int>> dist; // dist[i][j]: 位置(sx, sy)から位置(i, j)までの最小手数

int main() {
  int H, W; cin >> H >> W;
  int sh, sw, gh, gw; cin >> sh >> sw >> gh >> gw; sh--; sw--; gh--; gw--;
  Graph G(H);
  for (int i = 0; i < H; i++) cin >> G[i];
  dist.resize(H);
  for (int i = 0; i < H; i++) {
    dist[i].resize(W);
    dist[i].assign(W, -1);
  }

  dist[sh][sw] = 0;
  suspended.push(make_pair(sh, sw));
  while (!suspended.empty()) {
    int h, w;
    tie(h, w) = suspended.front(); suspended.pop();
    for (int dir = 0; dir < 4; dir++) {
      int nh = h + dh[dir];
      int nw = w + dw[dir];
      if (nh < 0 || H <= nh || nw < 0 || W <= nw) continue;
      if (dist[nh][nw] != -1) continue;
      if (G[nh][nw] == '#') continue;
      dist[nh][nw] = dist[h][w] + 1;
      suspended.push(make_pair(nh, nw));
    }
  }

  cout << dist[gh][gw] << endl;
  return 0;
}

# JOI2011 予選 5

ネズミの体力の初期値が$1$であり，チーズ$1$個ごとに体力が$1$増えるので，柔らかさ順にチーズを食べていくことになる．チーズ工場間の最短距離を求めていく．全対最短距離を求めるアルゴリズムを使っても良い．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <bits/stdc++.h>
using namespace std;

using Field = vector<string>;
Field F;
int H, W, N;
const int dh[4] = {1, 0, -1, 0};
const int dw[4] = {0, 1, 0, -1};

int BFS(pair<int, int> from, pair<int, int> to) {
  vector<vector<int>> dist(H, vector<int>(W, 1e8));
  queue<pair<int, int>> q;

  dist[from.first][from.second] = 0;
  q.push(from);

  while (!q.empty()) {
    auto p = q.front(); q.pop();
    int h = p.first;
    int w = p.second;
    if (pair<int, int>(h, w) == to) {
      return dist[h][w];
    }
    for (int dir = 0; dir < 4; dir++) {
      int nh = h + dh[dir];
      int nw = w + dw[dir];
      if (nh < 0 || H <= nh || nw < 0 || W <= nw) continue;
      if (F[nh][nw] == 'X') continue;
      if (dist[h][w] + 1 < dist[nh][nw]) {
        dist[nh][nw] = dist[h][w] + 1;
        q.push(pair<int, int>(nh, nw));
      }
    }
  }
  return -1; // should not reach here
}

int main() {
  cin >> H >> W >> N;
  F.resize(H);
  vector<pair<int, int>> factories(N+1);
  for (int i = 0; i < H; i++) cin >> F[i];
  for (int i = 0; i < H; i++) {
    for (int j = 0; j < W; j++) {
      if (F[i][j] == 'S') F[i][j] = '0';
      if ('0' <= F[i][j] && F[i][j] <= '9') {
        int idx = F[i][j] - '0';
        factories[idx] = pair<int, int>(i, j);
      }
    }
  }

  int ans = 0;
  for (int i = 0; i < N; i++) {
    ans += BFS(factories[i], factories[i+1]);
  }
  cout << ans << endl;
  return 0;
}

# JOI2012 予選 5

チョット変な座標系に対する BFS．建物のない区画に印をつけ，建物のない区画の周囲に建物が立っている区画があればその境界は色を塗ることになる．座標によって周囲 6 区画の，マス目位置が変わってくることに注意．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <bits/stdc++.h>
using namespace std;

const int odx[6] = {-1, -1,  0,  1,  1,  0};
const int ody[6] = { 0,  1,  1,  1,  0, -1};
const int edx[6] = {-1, -1,  0,  1,  1,  0};
const int edy[6] = {-1,  0,  1,  0, -1, -1};

int w, h;

int main() {
  cin >> w >> h;
  w += 2; h += 2;
  vector<vector<int>> a(h, vector<int>(w, -1));
  for (int i = 1; i < h-1; i++) {
    for (int j = 1; j < w-1; j++) {
      cin >> a[i][j];
    }
  }

  auto paint_BFS = [&](int sx, int sy) {
    queue<pair<int, int>> q;
    q.push(make_pair(sx, sy));
    while (!q.empty()) {
      auto p = q.front(); q.pop();
      int x = p.first, y = p.second;
      for (int dir = 0; dir < 6; dir++) {
        int nx, ny;
        if (x%2 == 1) {
          nx = x + odx[dir]; ny = y + ody[dir];
        } else {
          nx = x + edx[dir]; ny = y + edy[dir];
        }

        if (nx < 0 || h <= nx || ny < 0 || w <= ny) continue;
        if (a[nx][ny] == 1) continue;
        if (a[nx][ny] == -1) continue;
        a[nx][ny] = -1;
        q.push(make_pair(nx, ny));
      }
    }
  };

  for (int i = 0; i < h; i++) {
    for (int j = 0; j < w; j++) {
      if (a[i][j] == -1) paint_BFS(i, j);
    }
  }

  int ans = 0;
  {
    queue<pair<int, int>> q;
    q.push(make_pair(0, 0));
    while (!q.empty()) {
      auto p = q.front(); q.pop();
      int x = p.first, y = p.second;
      if (a[x][y] == 0) continue;
      for (int dir = 0; dir < 6; dir++) {
        int nx, ny;
        if (x%2 == 1) {
          nx = x + odx[dir]; ny = y + ody[dir];
        } else {
          nx = x + edx[dir]; ny = y + edy[dir];
        }

        if (nx < 0 || h <= nx || ny < 0 || w <= ny) continue;
        if (a[nx][ny] == 0) continue;
        if (a[nx][ny] == 1) {
          ans++;
          continue;
        }
        q.push(make_pair(nx, ny));
      }
      a[x][y] = 0;
    }
  }
  cout << ans << endl;
  return 0;
}

# AOJ 1166

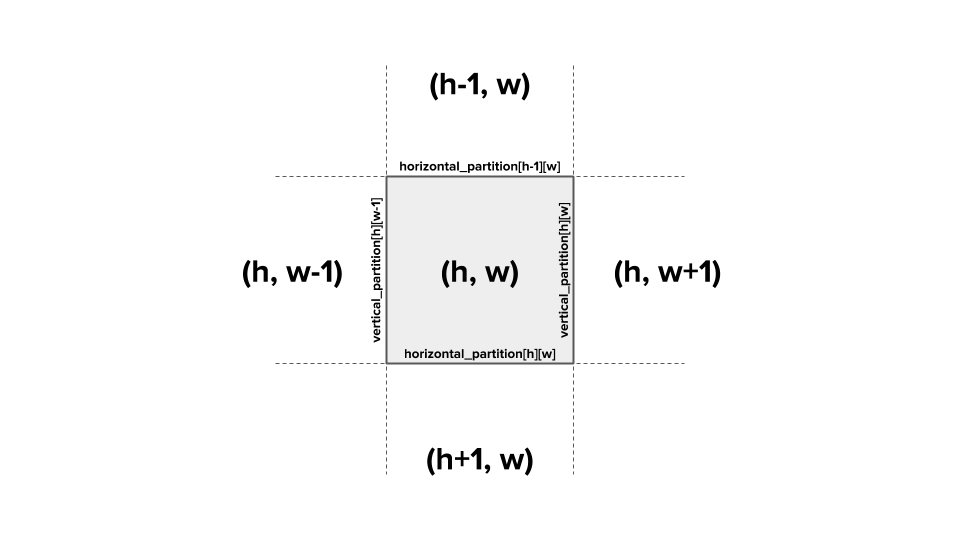
ややトリッキーな形で迷路情報が与えられる．内容は基本的な BFS に過ぎない．BFS のどこで迷路の情報を使うかというと，「隣接マスに行けるのか」を知るタイミングである．よって，縦横の仕切りの情報をそれぞれ別の形で持っておいて，隣接マスへの移動を考えるタイミングでその情報にアクセスするように実装する．

horizontal_partition，vertical_partitionという 2 つの配列で迷路情報を保持する．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>
using namespace std;

const int INF = 1001001;

const int dh[4] = {0, 1, 0, -1};
const int dw[4] = {1, 0, -1, 0};

int main() {
  while (1) {
    int W, H; cin >> W >> H;

    if (W == 0 && H == 0) break;

    int vertical_partition[H][W-1];
    int horizontal_partition[H-1][W];

    for (int i = 0; i < 2*H - 1; i++) {
      if (i%2 == 0) {
        for (int j = 0; j < W-1; j++) cin >> vertical_partition[i/2][j];
      } else {
        for (int j = 0; j < W; j++) cin >> horizontal_partition[i/2][j];
      }
    }

    int dist[H][W];
    for (int i = 0; i < H; i++) for (int j = 0; j < W; j++) dist[i][j] = INF;
    queue<pair<int, int>> q;

    dist[0][0] = 0;
    q.push(make_pair(0, 0));

    while (!q.empty()) {
      auto p = q.front(); q.pop();
      int h = p.first;
      int w = p.second;
      for (int dir = 0; dir < 4; dir++) {
        int nh = h + dh[dir];
        int nw = w + dw[dir];
        if (nh < 0 || H <= nh || nw < 0 || W <= nw) continue;
        if (nh == h+1 && nw == w && horizontal_partition[h][w] == 1) continue;
        if (nh == h && nw == w+1 && vertical_partition[h][w] == 1) continue;
        if (nh == h-1 && nw == w && horizontal_partition[h-1][w] == 1) continue;
        if (nh == h && nw == w-1 && vertical_partition[h][w-1] == 1) continue;
        if (dist[nh][nw] != INF) continue;
        dist[nh][nw] = dist[h][w] + 1;
        q.push(make_pair(nh, nw));
      }
    }
    cout <<  (dist[H-1][W-1] == INF ? 0 : dist[H-1][W-1] + 1) << endl;
  }
  return 0;
}

# ABC 88 D

要するに，$(1, 1)$から$(H, W)$まで最短経路で（＝通る白いマスの数が最小な経路で）いけば，それ以外のマスは黒に塗ることができ得点を最大化できる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <bits/stdc++.h>
using namespace std;

const int dh[4] = {1, 0, -1, 0};
const int dw[4] = {0, 1, 0, -1};

using Graph = vector<string>;
queue<pair<int, int>> suspended;
vector<vector<int>> dist; // dist[i][j]: 位置(sx, sy)から位置(i, j)までの最小手数

int main() {
  int H, W; cin >> H >> W;
  Graph G(H);
  for (int i = 0; i < H; i++) cin >> G[i];
  dist.resize(H);
  for (int i = 0; i < H; i++) {
    dist[i].resize(W);
    dist[i].assign(W, -1);
  }

  dist[0][0] = 0;
  suspended.push(make_pair(0, 0));
  while (!suspended.empty()) {
    int h, w;
    tie(h, w) = suspended.front(); suspended.pop();
    for (int dir = 0; dir < 4; dir++) {
      int nh = h + dh[dir];
      int nw = w + dw[dir];
      if (nh < 0 || H <= nh || nw < 0 || W <= nw) continue;
      if (dist[nh][nw] != -1) continue;
      if (G[nh][nw] == '#') continue;
      dist[nh][nw] = dist[h][w] + 1;
      suspended.push(make_pair(nh, nw));
    }
  }
  int white = 0;
  int ans = 0;
  for (int i = 0; i < H; i++) {
      for (int j = 0; j < W; j++) {
          if (G[i][j] == '.') white++;
      }
  }
  if (dist[H-1][W-1] == -1) cout << -1 << endl;
  else cout << white - dist[H-1][W-1] - 1 << endl;
  return 0;
}