二分探索

# 二分探索

二分探索というと「ソート済み配列の中から目的の値を効率よく（具体的には$O(\log n)$）で探し出す手法」として説明されることが圧倒的で，ともすると，「二分探索はソート済み配列から値を探すためだけのアルゴリズム」と勘違いしてしまう．実際，僕もそう思っていた．

二分探索の「半分にしてサイズの小さい問題を解く」というエッセンスは実に多くの問題に適用することができる．一般化された二分探索とも言うべきか．

# 「ソート済み配列から目的のアイテムを探す」二分探索

まずは，「ソート済み配列から目的のアイテムを探す」という，よくある二分探索を実装してみる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
#include <bits/stdc++.h>
using namespace std;

vector<int> a = {1, 14, 32, 51, 51, 51, 243, 419, 750, 910};

int binary_search(int key) {
  int left = 0, right = (int)a.size() - 1;
  while (left <= right) {
    int mid = left + (right - left) / 2;
    if (a[mid] == key) return mid;
    else if (key < a[mid]) right = mid - 1;
    else if (a[mid] < key) left = mid + 1;
  }
  return -1;
}

int main() {
  cout << binary_search(51) << endl;
  cout << binary_search(0) << endl;
  return 0;
}

探索範囲を半分ずつ小さくしてくことで目的のものを見つけ出す．探索範囲が指数の速度で小さくなっていくので，探索対象がソートされていれば，$O(\log n)$で目的のアイテムを見つけ出すことができる．

二分探索の実装はちょっとややこしい．ループの終了条件とか，left・rightの更新ってどうしてたっけとか考えると直感的にスラスラ書ける感じではない．

# 「ソート済み配列に対して，目的のアイテム以上となる最小のインデックスを求める」二分探索

二分探索を「ソート済み配列から目的のアイテムを探す」ではなくて， 「ソート済み配列に対して，目的のアイテム以上となる最小のインデックスを求める」 とするだけで，二分探索をいろんな問題に適用することができるようになる．

「ソート済み配列に対する，目的のアイテム以上となる最小のインデックス」からは

目的のアイテムが，探索範囲内で何番目に小さいのかがわかる
目的のアイテムが探索範囲内に複数存在するなら，それらのうち最小のインデックスを取れる
「目的のアイテムより大きくなる最小のインデックス」を取れれば，探索範囲内にいくつ同じアイテムが存在するかを知ることができる

と，より多くの情報を計算することができるようになる．

このような探索の汎化の有用性は，例えばstd::lower_bound()関数・std::upper_bound()関数が標準テンプレートライブラリ内で提供されていることからもうかがい知ることができる．関数がどんな返り値を返すか次第で，その関数の便利度合いも変わってくる．

std::lower_bound()関数は，ソート済み配列aと目的のアイテムkeyを与えることで，key <= a[index]となる最小のindexを返す．

std::upper_bound()関数は，ソート済み配列aと目的のアイテムkeyを与えることで，key < a[index]となる最小のindexを返す．

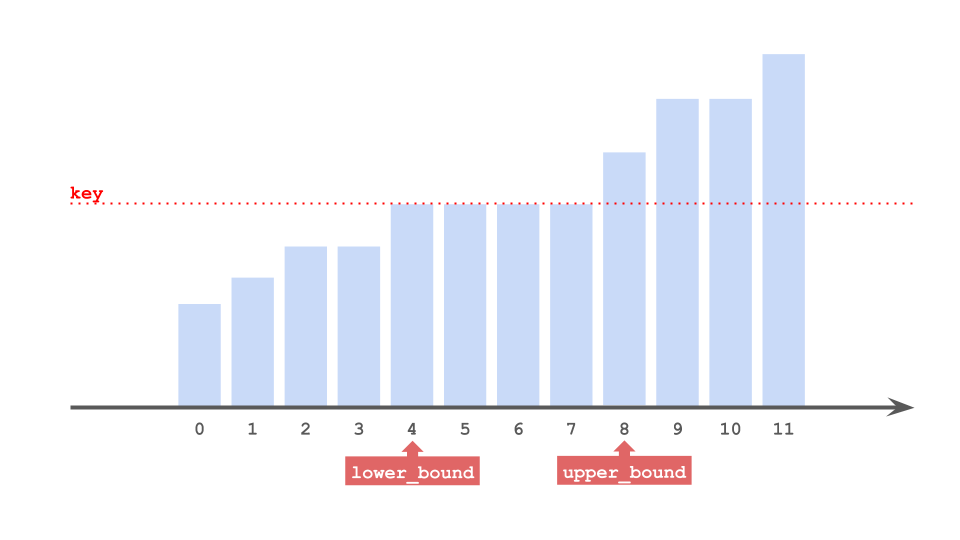
`std::lower_bound()`と`std:upper_bound()`

# 一般化された二分探索

「ソート済み配列に対して，目的のアイテム以上となる最小のインデックス」が得られたほうが便利ということがわかったところで，一般化された二分探索を考えると，二分探索は，「ある条件について，探索範囲において，その条件を満たすかどうかについて単調性が認められる（つまり，あるインデックスより小さいアイテムはその条件を満たさないけど，あるインデックス以上のアイテムはその条件を満たす）とき，その条件を満たす最小のアイテムを見つける」アルゴリズムとして一般化させることができる．二分探索をこのように捉えておくと，直感的な実装ができるようになる．

「ソート済み配列に対して，目的のアイテム以上となる最小のインデックスを求める」二分探索は次のように実装できる．このとき，「ある条件」とは「key以上」に相当し，配列に格納されているアイテムはソートされているので，条件を満たすか否かについての単調性が認められる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <bits/stdc++.h>
using namespace std;

vector<int> a = {1, 14, 32, 51, 51, 51, 243, 419, 750, 910};

bool is_ok(int index, int key) {
  if (key <= a[index]) return true;
  else return false;
}

int binary_search(int key) {
  int left = -1;
  int right = (int)a.size();

  while (1 < right - left) {
    int mid = left + (right - left) / 2;

    if (is_ok(mid, key)) right = mid;
    else left = mid;
  }
  return right;
}

int main() {
  cout << binary_search(51) << endl;
  cout << binary_search(0) << endl;
  return 0;
}

この実装では，

leftは「常に条件を満たさない要素のインデックス」
rightは「常に条件を満たす要素のインデックス」

とし，

right - left == 1となるまで，つまりleftとrightが隣り合うまで，条件を満たす・満たさないの境界を動かしていく

ことを繰り返している．最終的に，rightが「条件を満たす最小のインデックス」となる．

条件を満たすか否かの単調性が認められるとき，このように境界を移動させていくことで，条件を満たす最小のインデックスを求めることができる．一方で，単調性がない探索範囲においてこれを実行すると，条件を満たす・満たさないの境界の1つを見つけることができ，これは方程式の解の1つを求めるような場面で使える．

# めぐる式二分探索

上の実装では，left/rightの性質を考慮する必要があったが，それすら考慮することなく実装に落とし込むことができる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <bits/stdc++.h>
using namespace std;

vector<int> a = {1, 14, 32, 51, 51, 51, 243, 419, 750, 910};

bool is_ok(int index, int key) {
  if (key <= a[index]) return true;
  else return false;
}

int binary_search(int key) {
  int ng = -1;
  int ok = (int)a.size();

  while (1 < abs(ok - ng)) {
    int mid = (ok + ng) / 2;

    if (is_ok(mid, key)) ok = mid;
    else ng = mid;
  }
  return ok;
}

int main() {
  cout << binary_search(51) << endl;
  cout << binary_search(0) << endl;
  return 0;
}

# 二分探索の練習問題

# 解説

# ALDS 1-4 B

mapを使えば解決するけれども，二分探索でも解ける．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <bits/stdc++.h>
using namespace std;

int n, q;
vector<int> S(n), T(q);

bool is_ok(int index, int key) {
  if (key <= S[index]) return true;
  else return false;
}

int binary_search(int key) {
  int ng = -1;
  int ok = (int)S.size();

  while (1 < abs(ok - ng)) {
    int mid = (ok + ng) / 2;
    if (is_ok(mid, key)) ok = mid;
    else ng = mid;
  }
  return ok;
}

int main() {
  cin >> n;
  S.resize(n);
  for (int i = 0; i < n; i++) cin >> S[i];
  cin >> q;
  T.resize(q);
  for (int i = 0; i < q; i++) cin >> T[i];

  int cnt = 0;
  for (auto k : T) {
    if (0 <= binary_search(k) && binary_search(k) < n) cnt++;
  }
  cout << cnt << endl;
}

# JOI2009本選 2

ピザ屋さんと宅配先の位置関係（つまり，宅配先のすぐ両脇にあるピザ屋）がわかれば，宅配先の両隣のうちの近い方から宅配することで無駄なコストを掛けずにピザを運び届けることができる．両隣以外の店から宅配しようとしたら，その道中で両隣の店の一方に遭遇するはずだ．そりゃそうだ．なので，調べるべきは，宅配先のすぐ両隣にあるピザ屋がどれなのか．ピザ屋を，本店からの距離でソートしておいて，宅配先がどの位置に入るのかを二分探索で求める．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
using namespace std;

int main() {
  long long d;
  int n, m;
  cin >> d >> n >> m;
  vector<int> pizza_stores(n+1);
  for (int i = 1; i < n; i++) cin >> pizza_stores[i];
  pizza_stores[0] = 0;
  pizza_stores[n] = d;
  sort(pizza_stores.begin(), pizza_stores.end());
  vector<int> houses(m);
  for (int i = 0; i < m; i++) cin >> houses[i];
  long long  ans = 0;
  for (int i = 0; i < m; i++) {
    auto iter = lower_bound(pizza_stores.begin(), pizza_stores.end(), houses[i]);
    ans += min(abs(*iter - houses[i]), abs(*(iter - 1) - houses[i]));
  }
  cout << ans << endl;
  return 0;
}

# ABC 77 C

中部のパーツのサイズを$B_i$に固定すると，上部に使えるパーツのサイズは$B_i$より小さいもので，下部に使えるパーツのサイズは$B_i$より大きいものである．上部・下部に使えるパーツをそれぞれ大きさ順にソートしておいて二分探索によって，$B_i$より小さい・大きいパーツがいくつあるかを数えて掛け合わせれば，中部にサイズ$B_i$のパーツを使った祭壇の種類が得られるので，これを$i$について前通り試せば答えが求まる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
using namespace std;

int main() {
  int n; cin >> n;
  vector<long long> a(n), b(n), c(n);
  for (int i = 0; i < n; i++) cin >> a[i];
  for (int i = 0; i < n; i++) cin >> b[i];
  for (int i = 0; i < n; i++) cin >> c[i];
  sort(a.begin(), a.end());
  sort(b.begin(), b.end());
  sort(c.begin(), c.end());
  long long ans = 0;
  for (int i = 0; i < n; i++) {
    long long bi = b[i];
    auto aiter = lower_bound(a.begin(), a.end(), bi);
    auto citer = upper_bound(c.begin(), c.end(), bi);
    ans += distance(a.begin(), aiter) * distance(citer, c.end());
  }
  cout << ans << endl;
  return 0;
}

# ABC 34 D

風船の割り方の総数は$N!$通りだが，$1 \leq N \leq 100000$であることからぜんぶ探索するのでは間に合わない．

問題を「ペナルティの最小化問題」と捉えるのではなく，「全ての風船を高度$X$を超える前に割ることができるか」という判定問題として捉え，全ての風船を割ることができる高度$X$の最小値が求める答えとなる．

「$X$を固定したとき，全ての風船を割ることができるか」は高度$X$に到達するまでの猶予が短い風船から割る貪欲法で調べることができる．

一方で$X$の値は，「高度$X$以下で，全ての風船を割ることができるか」という条件を満たす最小のものとして二分探索によって決定することができる．「高度$X$以下で，全ての風船を割ることができるか」という条件は，ある値$H$未満の$X$に対しては偽となり，$H$以上の$X$に対して真となる単調性がある．「高度10cmまでにぜんぶの風船を割れ」と言われても無理だけど，「高度1000kmまでにぜんぶの風船を割れ」と言われても余裕ということ．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>
using namespace std;

using ll = long long;
ll N;
ll H[100010], S[100010];

int main() {
  cin >> N;
  for (int i = 0; i < N; i++) cin >> H[i] >> S[i];
  ll ng = 0;
  ll ok = 1e15;
  vector<ll> hist(N); // hist[i]: 時刻iまでに割らなければならない風船の個数
  while (1 < abs(ok - ng)) {
    ll mid = (ok + ng) / 2;
    bool flag = true;

    // 以下でbool is_ok(mid){...}を計算
    for (int i = 0; i < N; i++) hist[i] = 0;
    for (int i = 0; i < N; i++) {
      if (mid < H[i]) flag = false; // 時刻0ですでに高度midより上に風船がある
      ll remind_time = (mid - H[i]) / S[i]; // 高度midに到達するまでの時間的猶予
      if (remind_time < 0) {
        flag = false;
        break;
      }
      hist[min(remind_time, N-1)]++;
    }
    for (int i = 1; i < N; i++) hist[i] += hist[i-1];
    for (int i = 0; i < N; i++) {
      if (i+1 < hist[i]) flag = false; // 時刻iまでに割れる最大の風船の個数はi+1個（時刻0のときに1つ割ることに注意）
    }

    if (flag) ok = mid;
    else ng = mid;
  }
  cout << ok << endl;
  return 0;
}

# JOI2008 本選3

矢のあたり方の総数は，（「矢を投げない」を「$0$点の的に当たる」と考えて，）$(N+1)^4$通りあるので，ぜんぶを調べ上げれば原理的に解ける．しかし$N$の制約からこれでは満点は取れない．この解法の無駄なところは，4本全ての矢を投げないと得点を計算できないとしている点である．例えば，2本投げた時点ですでに当たった的の合計が$M$を超えてしまえば最終得点は（残り2本の矢を投げるまでもなく）$0$に決定する．そこで，矢を2本ごとに投げることを一つの単位として最大得点を調べ上げることにする．具体的には，まず最初の2本の矢を投げたときに得られる合計得点$Q_1$（最大で$(N+1)^2$通りの値）を計算し昇順にソートしておく．続く2本の矢を投げたときの得点$Q_2$を，条件「$Q_1 + Q_2 \leq M$」を満たす最大の値として二分探索する．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>
using namespace std;

int main() {
  int N; long long M; cin >> N >> M;
  vector<long long> P(N);
  for (int i = 0; i < N; i++) cin >> P[i];
  P.push_back(0LL);
  N += 1;

  vector<long long> Q;
  set<long long> tmp;
  for (int i = 0; i < N+1; i++) {
    for (int j = i; j < N+1; j++) {
      tmp.insert(P[i] + P[j]);
    }
  }
  for (auto iter = tmp.begin(); iter != tmp.end(); iter++) Q.push_back(*iter);
  sort(Q.begin(), Q.end());

  long long ans = -1;
  for (int i = 0; i < (int)Q.size(); i++) {
    long long total = Q[i];
    if (M < total) break;
    int ok = -1;
    int ng = (int)Q.size();
    while (1 < abs(ok - ng)) {
      int mid = (ok + ng) / 2;
      bool is_ok = true;
      if (M < total + Q[mid]) is_ok = false;
      if (is_ok) ok = mid;
      else ng = mid;
    }
    total += Q[ok];
    ans = max(ans, total);
  }
  cout << ans << endl;
  return 0;
}

# 最後に

二分探索：ソート済みの配列に対して，条件$X$を満たす最小のアイテムを探し当てる